Multiobjective Programming for Type-2 Hierarchical Fuzzy Inference Trees
Paper and Code
May 16, 2017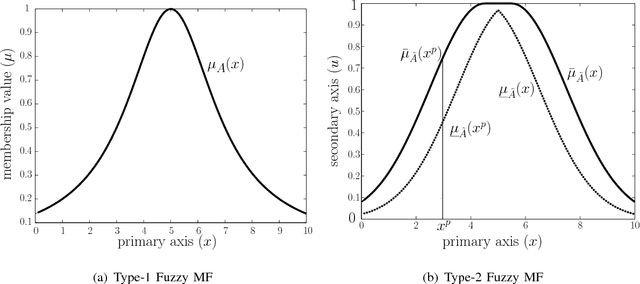
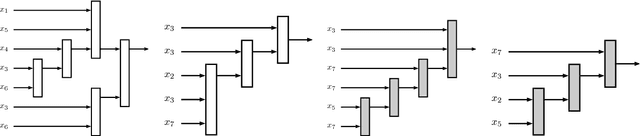
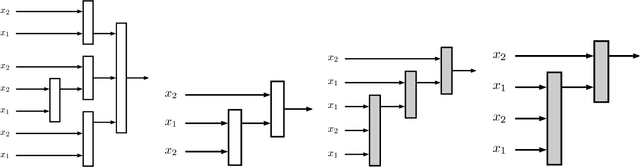
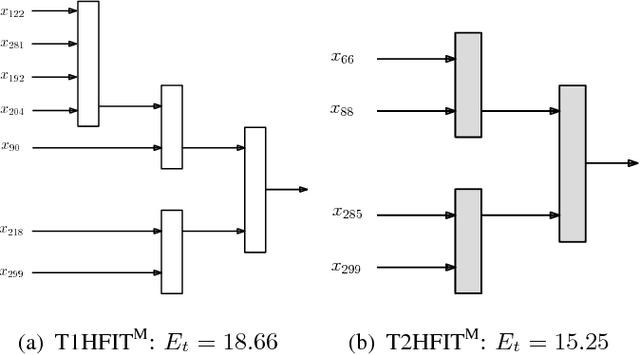
This paper proposes a design of hierarchical fuzzy inference tree (HFIT). An HFIT produces an optimum treelike structure, i.e., a natural hierarchical structure that accommodates simplicity by combining several low-dimensional fuzzy inference systems (FISs). Such a natural hierarchical structure provides a high degree of approximation accuracy. The construction of HFIT takes place in two phases. Firstly, a nondominated sorting based multiobjective genetic programming (MOGP) is applied to obtain a simple tree structure (a low complexity model) with a high accuracy. Secondly, the differential evolution algorithm is applied to optimize the obtained tree's parameters. In the derived tree, each node acquires a different input's combination, where the evolutionary process governs the input's combination. Hence, HFIT nodes are heterogeneous in nature, which leads to a high diversity among the rules generated by the HFIT. Additionally, the HFIT provides an automatic feature selection because it uses MOGP for the tree's structural optimization that accepts inputs only relevant to the knowledge contained in data. The HFIT was studied in the context of both type-1 and type-2 FISs, and its performance was evaluated through six application problems. Moreover, the proposed multiobjective HFIT was compared both theoretically and empirically with recently proposed FISs methods from the literature, such as McIT2FIS, TSCIT2FNN, SIT2FNN, RIT2FNS-WB, eT2FIS, MRIT2NFS, IT2FNN-SVR, etc. From the obtained results, it was found that the HFIT provided less complex and highly accurate models compared to the models produced by the most of other methods. Hence, the proposed HFIT is an efficient and competitive alternative to the other FISs for function approximation and feature selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge