Multi-view Low-rank Sparse Subspace Clustering
Paper and Code
Aug 29, 2017
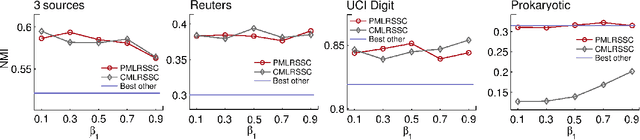
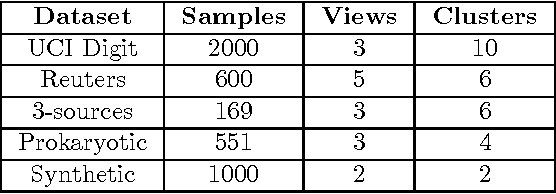
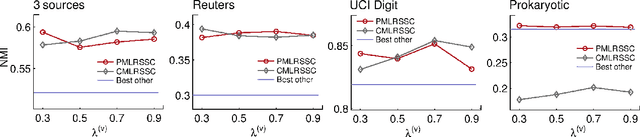
Most existing approaches address multi-view subspace clustering problem by constructing the affinity matrix on each view separately and afterwards propose how to extend spectral clustering algorithm to handle multi-view data. This paper presents an approach to multi-view subspace clustering that learns a joint subspace representation by constructing affinity matrix shared among all views. Relying on the importance of both low-rank and sparsity constraints in the construction of the affinity matrix, we introduce the objective that balances between the agreement across different views, while at the same time encourages sparsity and low-rankness of the solution. Related low-rank and sparsity constrained optimization problem is for each view solved using the alternating direction method of multipliers. Furthermore, we extend our approach to cluster data drawn from nonlinear subspaces by solving the corresponding problem in a reproducing kernel Hilbert space. The proposed algorithm outperforms state-of-the-art multi-view subspace clustering algorithms on one synthetic and four real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge