Multi-view Kernel Completion
Paper and Code
Feb 08, 2016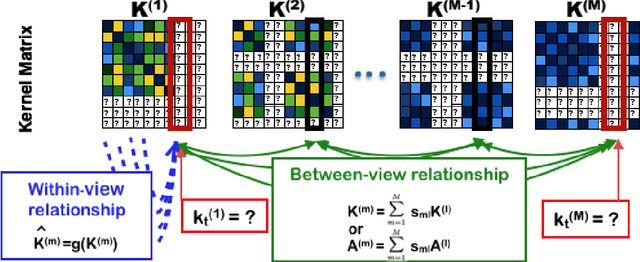
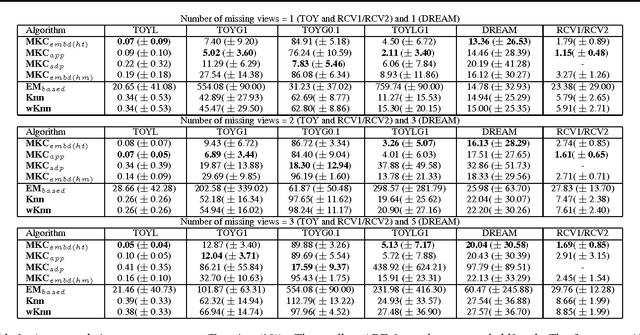
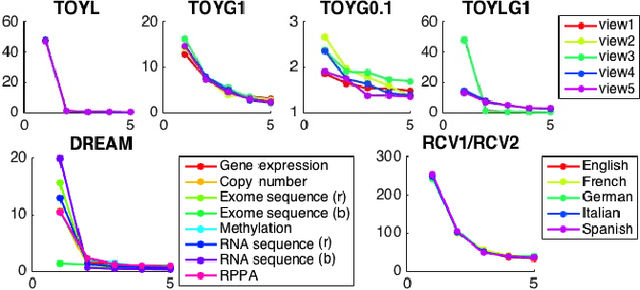
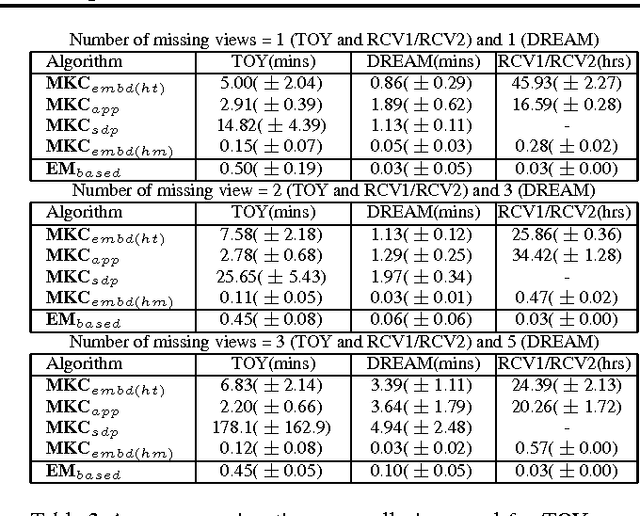
In this paper, we introduce the first method that (1) can complete kernel matrices with completely missing rows and columns as opposed to individual missing kernel values, (2) does not require any of the kernels to be complete a priori, and (3) can tackle non-linear kernels. These aspects are necessary in practical applications such as integrating legacy data sets, learning under sensor failures and learning when measurements are costly for some of the views. The proposed approach predicts missing rows by modelling both within-view and between-view relationships among kernel values. We show, both on simulated data and real world data, that the proposed method outperforms existing techniques in the restricted settings where they are available, and extends applicability to new settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge