Multi-Tier Federated Learning for Vertically Partitioned Data
Paper and Code
Feb 06, 2021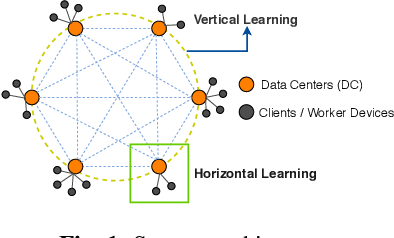
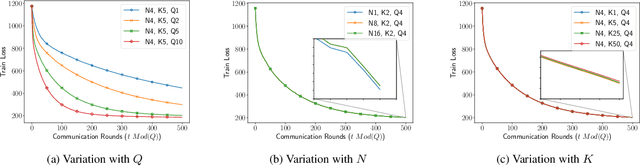
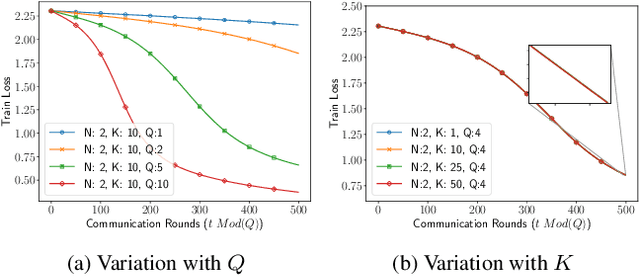
We consider decentralized model training in tiered communication networks. Our network model consists of a set of silos, each holding a vertical partition of the data. Each silo contains a hub and a set of clients, with the silo's vertical data shard partitioned horizontally across its clients. We propose Tiered Decentralized Coordinate Descent (TDCD), a communication-efficient decentralized training algorithm for such two-tiered networks. To reduce communication overhead, the clients in each silo perform multiple local gradient steps before sharing updates with their hub. Each hub adjusts its coordinates by averaging its workers' updates, and then hubs exchange intermediate updates with one another. We present a theoretical analysis of our algorithm and show the dependence of the convergence rate on the number of vertical partitions, the number of local updates, and the number of clients in each hub. We further validate our approach empirically via simulation-based experiments using a variety of datasets and both convex and non-convex objectives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge