Multi-Task Kernel Null-Space for One-Class Classification
Paper and Code
May 22, 2019
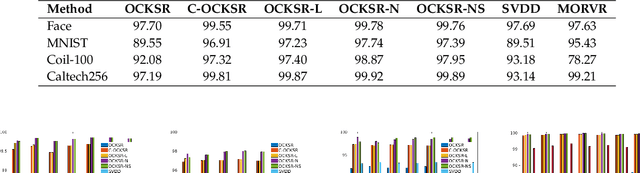
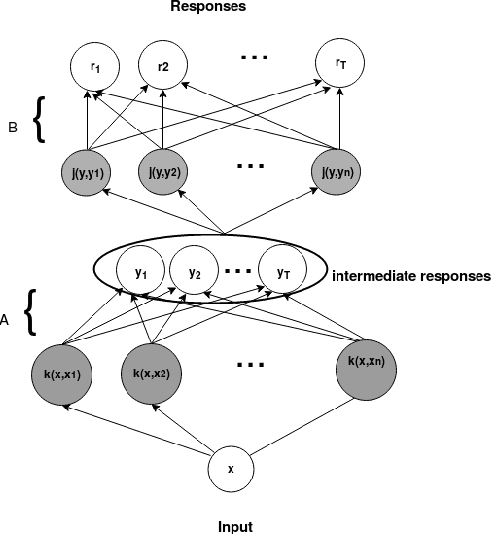

The one-class kernel spectral regression (OC-KSR), the regression-based formulation of the kernel null-space approach has been found to be an effective Fisher criterion-based methodology for one-class classification (OCC), achieving state-of-the-art performance in one-class classification while providing relatively high robustness against data corruption. This work extends the OC-KSR methodology to a multi-task setting where multiple one-class problems share information for improved performance. By viewing the multi-task structure learning problem as one of compositional function learning, first, the OC-KSR method is extended to learn multiple tasks' structure \textit{linearly} by posing it as an instantiation of the separable kernel learning problem in a vector-valued reproducing kernel Hilbert space where an output kernel encodes tasks' structure while another kernel captures input similarities. Next, a non-linear structure learning mechanism is proposed which captures multiple tasks' relationships \textit{non-linearly} via an output kernel. The non-linear structure learning method is then extended to a sparse setting where different tasks compete in an output composition mechanism, leading to a sparse non-linear structure among multiple problems. Through extensive experiments on different data sets, the merits of the proposed multi-task kernel null-space techniques are verified against the baseline as well as other existing multi-task one-class learning techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge