Multi-goal path planning using multiple random trees
Paper and Code
Jun 07, 2021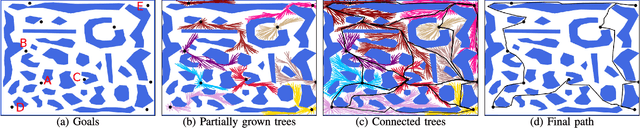
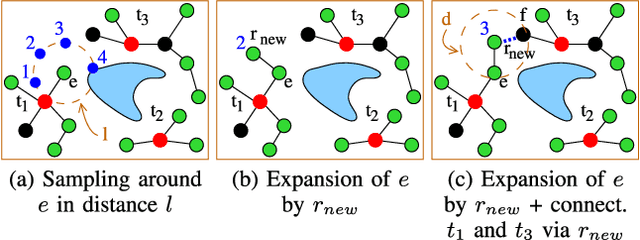
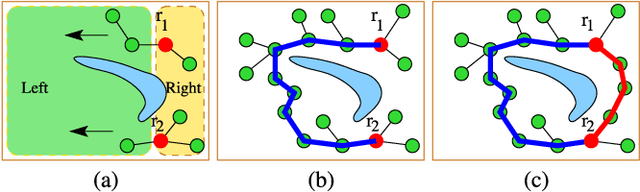
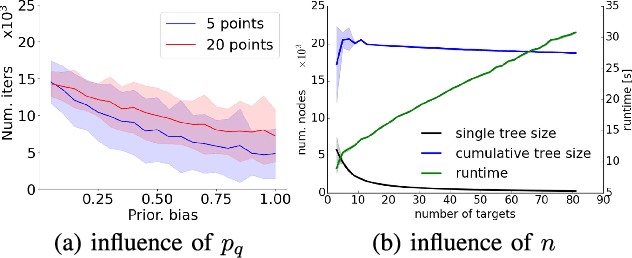
In this paper, we propose a novel sampling-based planner for multi-goal path planning among obstacles, where the objective is to visit predefined target locations while minimizing the travel costs. The order of visiting the targets is often achieved by solving the Traveling Salesman Problem (TSP) or its variants. TSP requires to define costs between the individual targets, which - in a map with obstacles - requires to compute mutual paths between the targets. These paths, found by path planning, are used both to define the costs (e.g., based on their length or time-to-traverse) and also they define paths that are later used in the final solution. To enable TSP finding a good-quality solution, it is necessary to find these target-to-target paths as short as possible. We propose a sampling-based planner called Space-Filling Forest (SFF*) that solves the part of finding collision-free paths. SFF* uses multiple trees (forest) constructed gradually and simultaneously from the targets and attempts to find connections with other trees to form the paths. Unlike Rapidly-exploring Random Tree (RRT), which uses the nearest-neighbor rule for selecting nodes for expansion, SFF* maintains an explicit list of nodes for expansion. Individual trees are grown in a RRT* manner, i.e., with rewiring the nodes to minimize their cost. Computational results show that SFF* provides shorter target-to-target paths than existing approaches, and consequently, the final TSP solutions also have a lower cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge