Multi-Attribute Proportional Representation
Paper and Code
Sep 11, 2015
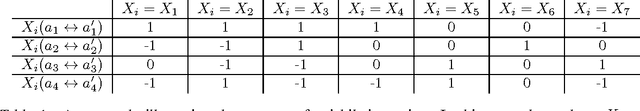
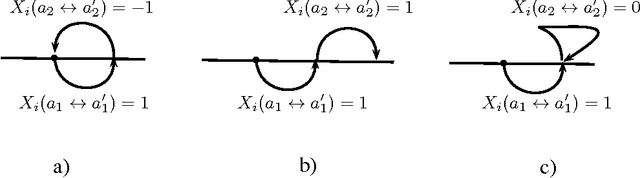
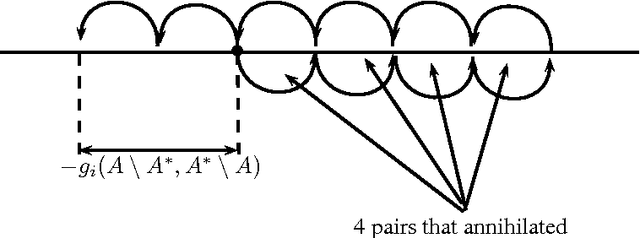
We consider the following problem in which a given number of items has to be chosen from a predefined set. Each item is described by a vector of attributes and for each attribute there is a desired distribution that the selected set should have. We look for a set that fits as much as possible the desired distributions on all attributes. Examples of applications include choosing members of a representative committee, where candidates are described by attributes such as sex, age and profession, and where we look for a committee that for each attribute offers a certain representation, i.e., a single committee that contains a certain number of young and old people, certain number of men and women, certain number of people with different professions, etc. With a single attribute the problem collapses to the apportionment problem for party-list proportional representation systems (in such case the value of the single attribute would be a political affiliation of a candidate). We study the properties of the associated subset selection rules, as well as their computation complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge