Motion Planning as Online Learning: A Multi-Armed Bandit Approach to Kinodynamic Sampling-Based Planning
Paper and Code
Aug 26, 2023
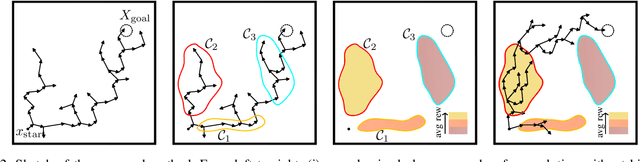

Kinodynamic motion planners allow robots to perform complex manipulation tasks under dynamics constraints or with black-box models. However, they struggle to find high-quality solutions, especially when a steering function is unavailable. This paper presents a novel approach that adaptively biases the sampling distribution to improve the planner's performance. The key contribution is to formulate the sampling bias problem as a non-stationary multi-armed bandit problem, where the arms of the bandit correspond to sets of possible transitions. High-reward regions are identified by clustering transitions from sequential runs of kinodynamic RRT and a bandit algorithm decides what region to sample at each timestep. The paper demonstrates the approach on several simulated examples as well as a 7-degree-of-freedom manipulation task with dynamics uncertainty, suggesting that the approach finds better solutions faster and leads to a higher success rate in execution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge