Motif-Based Spectral Clustering of Weighted Directed Networks

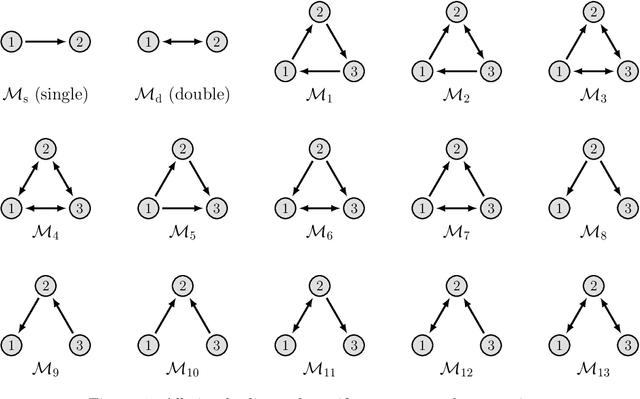
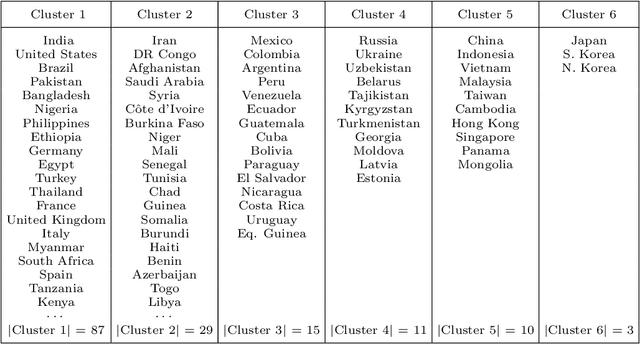
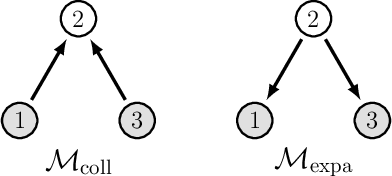
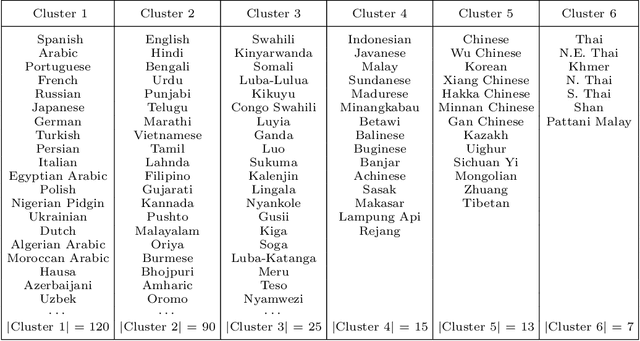
Clustering is an essential technique for network analysis, with applications in a diverse range of fields. Although spectral clustering is a popular and effective method, it fails to consider higher-order structure and can perform poorly on directed networks. One approach is to capture and cluster higher-order structures using motif adjacency matrices. However, current formulations fail to take edge weights into account, and thus are somewhat limited when weight is a key component of the network under study. We address these shortcomings by exploring motif-based weighted spectral clustering methods. We present new and computationally useful matrix formulae for motif adjacency matrices on weighted networks, which can be used to construct efficient algorithms for any anchored or non-anchored motif on three nodes. In a very sparse regime, our proposed method can handle graphs with five million nodes and tens of millions of edges in under ten minutes. We further use our framework to construct a motif-based approach for clustering bipartite networks. We provide comprehensive experimental results, demonstrating (i) the scalability of our approach, (ii) advantages of higher-order clustering on synthetic examples, and (iii) the effectiveness of our techniques on a variety of real world data sets. We conclude that motif-based spectral clustering is a valuable tool for analysis of directed and bipartite weighted networks, which is also scalable and easy to implement.