Monte-Carlo Planning: Theoretically Fast Convergence Meets Practical Efficiency
Paper and Code
Sep 26, 2013
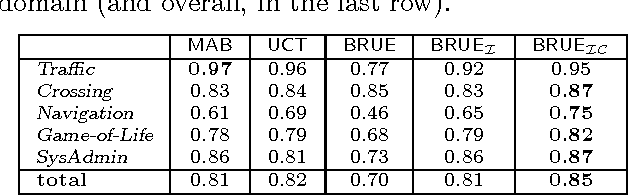

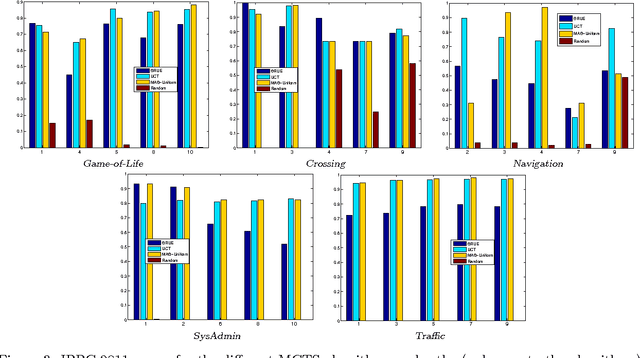
Popular Monte-Carlo tree search (MCTS) algorithms for online planning, such as epsilon-greedy tree search and UCT, aim at rapidly identifying a reasonably good action, but provide rather poor worst-case guarantees on performance improvement over time. In contrast, a recently introduced MCTS algorithm BRUE guarantees exponential-rate improvement over time, yet it is not geared towards identifying reasonably good choices right at the go. We take a stand on the individual strengths of these two classes of algorithms, and show how they can be effectively connected. We then rationalize a principle of "selective tree expansion", and suggest a concrete implementation of this principle within MCTS. The resulting algorithm,s favorably compete with other MCTS algorithms under short planning times, while preserving the attractive convergence properties of BRUE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge