Monotonicity Regularization: Improved Penalties and Novel Applications to Disentangled Representation Learning and Robust Classification
Paper and Code
May 17, 2022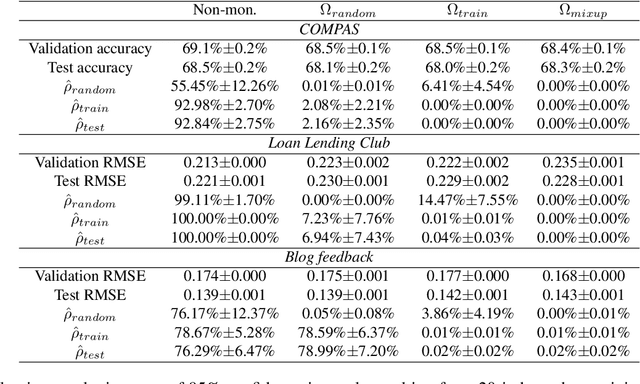


We study settings where gradient penalties are used alongside risk minimization with the goal of obtaining predictors satisfying different notions of monotonicity. Specifically, we present two sets of contributions. In the first part of the paper, we show that different choices of penalties define the regions of the input space where the property is observed. As such, previous methods result in models that are monotonic only in a small volume of the input space. We thus propose an approach that uses mixtures of training instances and random points to populate the space and enforce the penalty in a much larger region. As a second set of contributions, we introduce regularization strategies that enforce other notions of monotonicity in different settings. In this case, we consider applications, such as image classification and generative modeling, where monotonicity is not a hard constraint but can help improve some aspects of the model. Namely, we show that inducing monotonicity can be beneficial in applications such as: (1) allowing for controllable data generation, (2) defining strategies to detect anomalous data, and (3) generating explanations for predictions. Our proposed approaches do not introduce relevant computational overhead while leading to efficient procedures that provide extra benefits over baseline models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge