Monocular 3D Pose Recovery via Nonconvex Sparsity with Theoretical Analysis
Paper and Code
Dec 29, 2018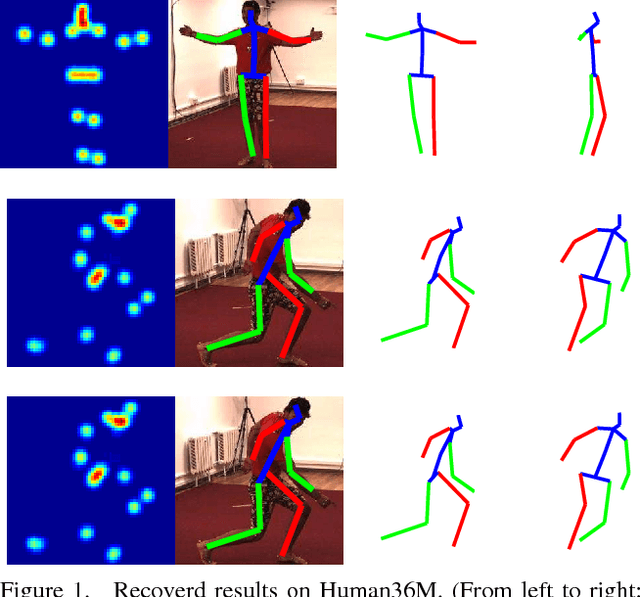
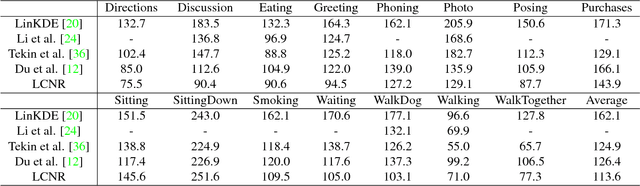
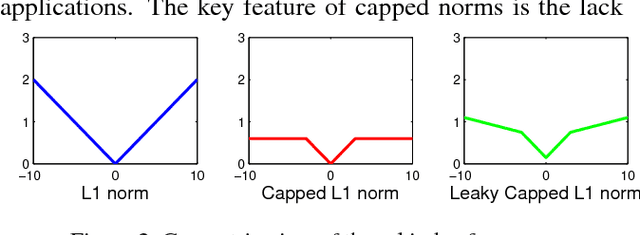

For recovering 3D object poses from 2D images, a prevalent method is to pre-train an over-complete dictionary $\mathcal D=\{B_i\}_i^D$ of 3D basis poses. During testing, the detected 2D pose $Y$ is matched to dictionary by $Y \approx \sum_i M_i B_i$ where $\{M_i\}_i^D=\{c_i \Pi R_i\}$, by estimating the rotation $R_i$, projection $\Pi$ and sparse combination coefficients $c \in \mathbb R_{+}^D$. In this paper, we propose non-convex regularization $H(c)$ to learn coefficients $c$, including novel leaky capped $\ell_1$-norm regularization (LCNR), \begin{align*} H(c)=\alpha \sum_{i } \min(|c_i|,\tau)+ \beta \sum_{i } \max(| c_i|,\tau), \end{align*} where $0\leq \beta \leq \alpha$ and $0<\tau$ is a certain threshold, so the invalid components smaller than $\tau$ are composed with larger regularization and other valid components with smaller regularization. We propose a multi-stage optimizer with convex relaxation and ADMM. We prove that the estimation error $\mathcal L(l)$ decays w.r.t. the stages $l$, \begin{align*} Pr\left(\mathcal L(l) < \rho^{l-1} \mathcal L(0) + \delta \right) \geq 1- \epsilon, \end{align*} where $0< \rho <1, 0<\delta, 0<\epsilon \ll 1$. Experiments on large 3D human datasets like H36M are conducted to support our improvement upon previous approaches. To the best of our knowledge, this is the first theoretical analysis in this line of research, to understand how the recovery error is affected by fundamental factors, e.g. dictionary size, observation noises, optimization times. We characterize the trade-off between speed and accuracy towards real-time inference in applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge