Monkey Optimization System with Active Membranes: A New Meta-heuristic Optimization System
Paper and Code
Sep 30, 2019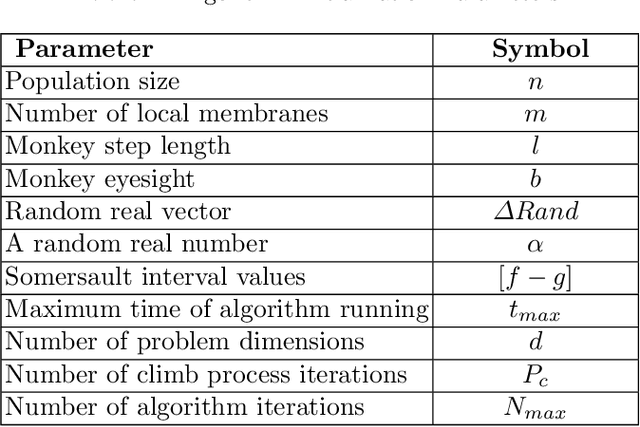
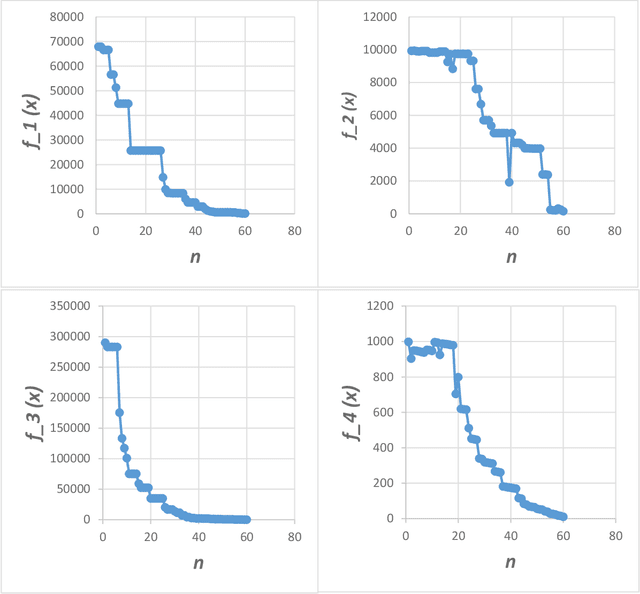
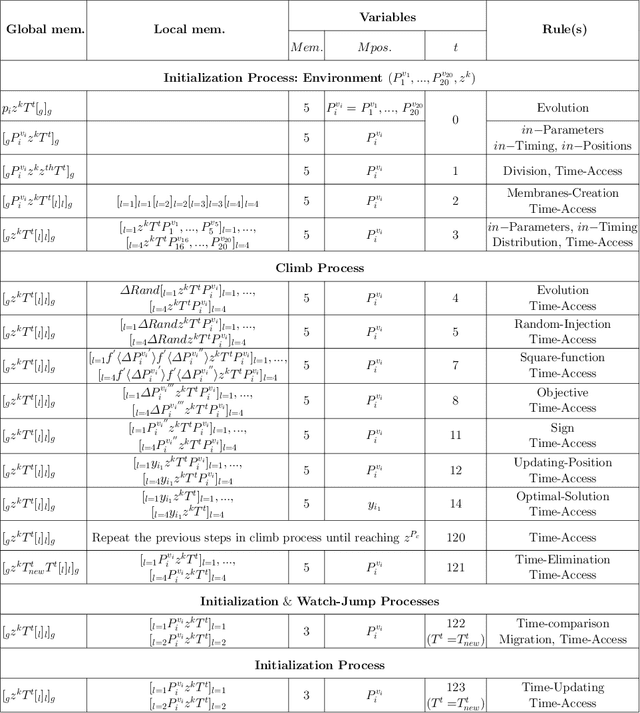
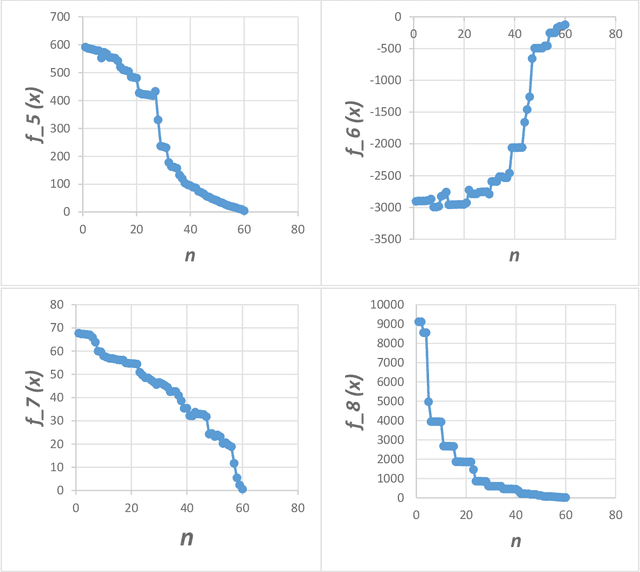
Optimization techniques, used to get the optimal solution in search spaces, have not solved the time-consuming problem. The objective of this study is to tackle the sequential processing problem in Monkey Algorithm and simulating the natural parallel behavior of monkeys. Therefore, a P system with active membranes is constructed by providing a codification for Monkey Algorithm within the context of a cell-like P system, defining accordingly the elements of the model - membrane structure, objects, rules and the behavior of it. The proposed algorithm has modeled the natural behavior of climb process using separate membranes, rather than the original algorithm. Moreover, it introduced the membrane migration process to select the best solution and the time stamp was added as an additional stopping criterion to control the timing of the algorithm. The results indicate a substantial solution for the time consumption problem, significant representation of the natural behavior of monkeys, and considerable chance to reach the best solution in the context of meta-heuristics purpose. In addition, experiments use the commonly used benchmark functions to test the performance of the algorithm as well as the expected time of the proposed P Monkey optimization algorithm and the traditional Monkey Algorithm running on population size. The unit times are calculated based on the complexity of algorithms, where P Monkey takes a time unit to fire rule(s) over a population size n; as soon as, Monkey Algorithm takes a time unit to run a step every mathematical equation over a population size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge