Modular Semantics and Characteristics for Bipolar Weighted Argumentation Graphs
Paper and Code
Sep 26, 2018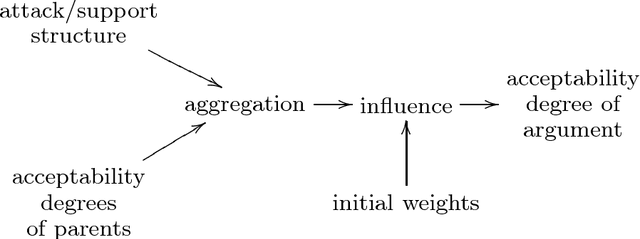
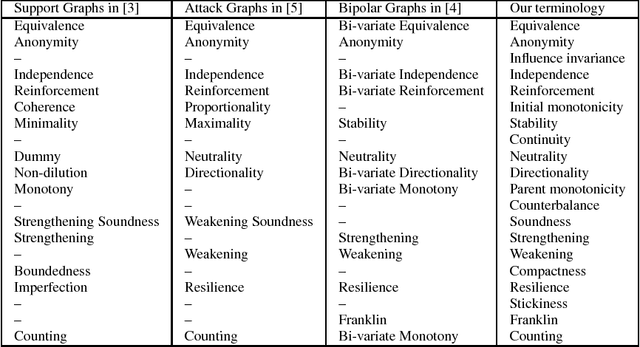

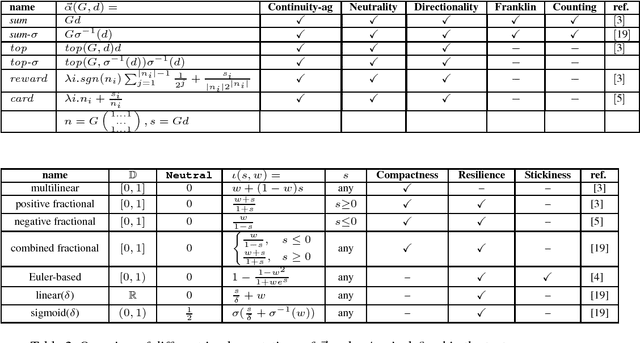
This paper addresses the semantics of weighted argumentation graphs that are bipolar, i.e. contain both attacks and supports for arguments. It builds on previous work by Amgoud, Ben-Naim et. al. We study the various characteristics of acceptability semantics that have been introduced in these works, and introduce the notion of a modular acceptability semantics. A semantics is modular if it cleanly separates aggregation of attacking and supporting arguments (for a given argument $a$) from the computation of their influence on $a$'s initial weight. We show that the various semantics for bipolar argumentation graphs from the literature may be analysed as a composition of an aggregation function with an influence function. Based on this modular framework, we prove general convergence and divergence theorems. We demonstrate that all well-behaved modular acceptability semantics converge for all acyclic graphs and that no sum-based semantics can converge for all graphs. In particular, we show divergence of Euler-based semantics (Amgoud et al.) for certain cyclic graphs. Further, we provide the first semantics for bipolar weighted graphs that converges for all graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge