Modular Conformal Calibration
Paper and Code
Jul 05, 2022

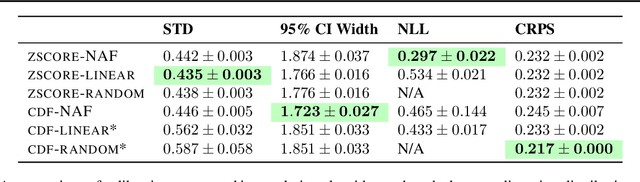

Uncertainty estimates must be calibrated (i.e., accurate) and sharp (i.e., informative) in order to be useful. This has motivated a variety of methods for recalibration, which use held-out data to turn an uncalibrated model into a calibrated model. However, the applicability of existing methods is limited due to their assumption that the original model is also a probabilistic model. We introduce a versatile class of algorithms for recalibration in regression that we call Modular Conformal Calibration (MCC). This framework allows one to transform any regression model into a calibrated probabilistic model. The modular design of MCC allows us to make simple adjustments to existing algorithms that enable well-behaved distribution predictions. We also provide finite-sample calibration guarantees for MCC algorithms. Our framework recovers isotonic recalibration, conformal calibration, and conformal interval prediction, implying that our theoretical results apply to those methods as well. Finally, we conduct an empirical study of MCC on 17 regression datasets. Our results show that new algorithms designed in our framework achieve near-perfect calibration and improve sharpness relative to existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge