$γ$-Models: Generative Temporal Difference Learning for Infinite-Horizon Prediction

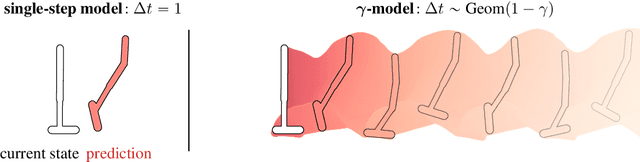
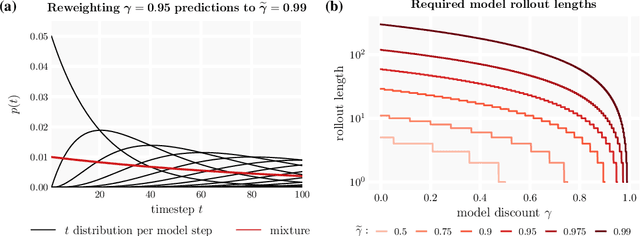
We introduce the $\gamma$-model, a predictive model of environment dynamics with an infinite probabilistic horizon. Replacing standard single-step models with $\gamma$-models leads to generalizations of the procedures that form the foundation of model-based control, including the model rollout and model-based value estimation. The $\gamma$-model, trained with a generative reinterpretation of temporal difference learning, is a natural continuous analogue of the successor representation and a hybrid between model-free and model-based mechanisms. Like a value function, it contains information about the long-term future; like a standard predictive model, it is independent of task reward. We instantiate the $\gamma$-model as both a generative adversarial network and normalizing flow, discuss how its training reflects an inescapable tradeoff between training-time and testing-time compounding errors, and empirically investigate its utility for prediction and control.