Modelling and Quantifying Membership Information Leakage in Machine Learning
Paper and Code
Jan 29, 2020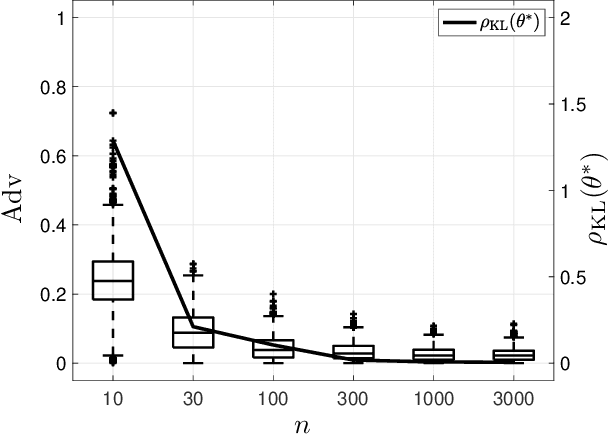
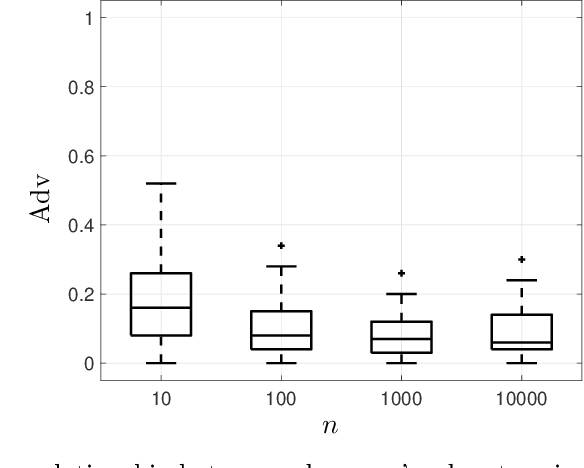
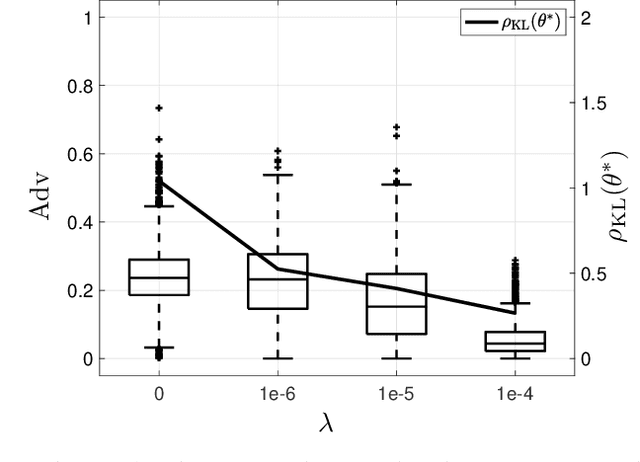
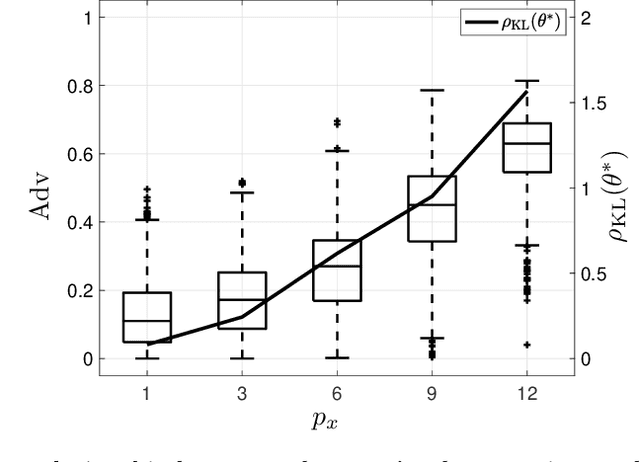
Machine learning models have been shown to be vulnerable to membership inference attacks, i.e., inferring whether individuals' data have been used for training models. The lack of understanding about factors contributing success of these attacks motivates the need for modelling membership information leakage using information theory and for investigating properties of machine learning models and training algorithms that can reduce membership information leakage. We use conditional mutual information leakage to measure the amount of information leakage from the trained machine learning model about the presence of an individual in the training dataset. We devise an upper bound for this measure of information leakage using Kullback--Leibler divergence that is more amenable to numerical computation. We prove a direct relationship between the Kullback--Leibler membership information leakage and the probability of success for a hypothesis-testing adversary examining whether a particular data record belongs to the training dataset of a machine learning model. We show that the mutual information leakage is a decreasing function of the training dataset size and the regularization weight. We also prove that, if the sensitivity of the machine learning model (defined in terms of the derivatives of the fitness with respect to model parameters) is high, more membership information is potentially leaked. This illustrates that complex models, such as deep neural networks, are more susceptible to membership inference attacks in comparison to simpler models with fewer degrees of freedom. We show that the amount of the membership information leakage is reduced by $\mathcal{O}(\log^{1/2}(\delta^{-1})\epsilon^{-1})$ when using Gaussian $(\epsilon,\delta)$-differentially-private additive noises.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge