Modelling and Fast Terminal Sliding Mode Control for Mirror-based Pointing Systems
Paper and Code
Dec 19, 2018

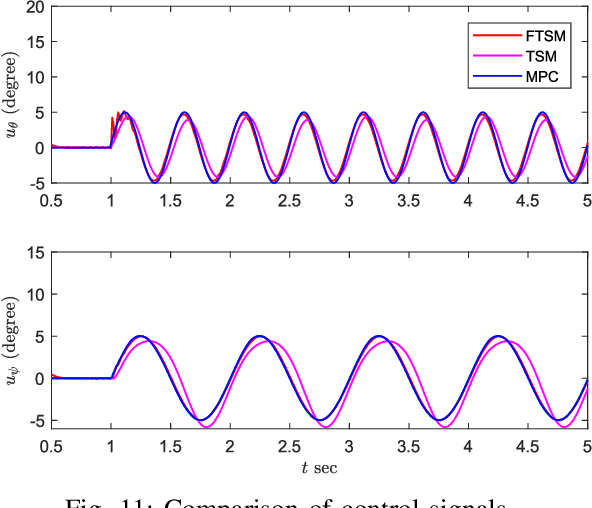

In this paper, we present a new discrete-time Fast Terminal Sliding Mode (FTSM) controller for mirror-based pointing systems. We first derive the decoupled model of those systems and then estimate the parameters using a nonlinear least-square identification method. Based on the derived model, we design a FTSM sliding manifold in the continuous domain. We then exploit the Euler discretization on the designed FTSM sliding surfaces to synthesize a discrete-time controller. Furthermore, we improve the transient dynamics of the sliding surface by adding a linear term. Finally, we prove the stability of the proposed controller based on the Sarpturk reaching condition. Extensive simulations, followed by comparisons with the Terminal Sliding Mode (TSM) and Model Predictive Control (MPC) have been carried out to evaluate the effectiveness of the proposed approach. A comparative study with data obtained from a real-time experiment was also conducted. The results indicate the advantage of the proposed method over the other techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge