Modeling the Machine Learning Multiverse
Paper and Code
Jun 13, 2022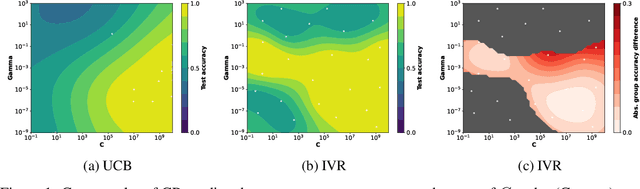
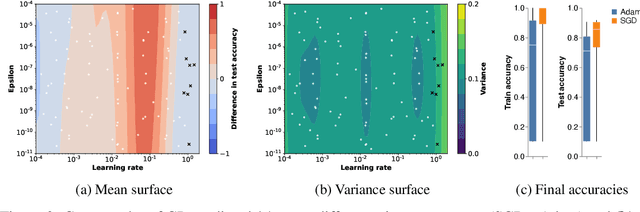
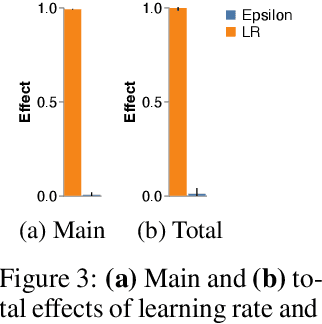
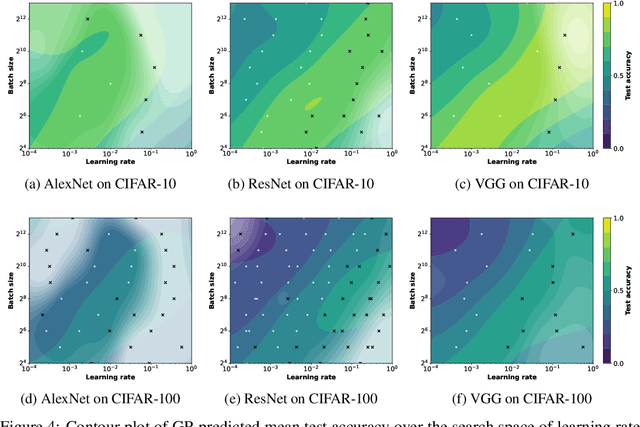
Amid mounting concern about the reliability and credibility of machine learning research, we present a principled framework for making robust and generalizable claims: the Multiverse Analysis. Our framework builds upon the Multiverse Analysis (Steegen et al., 2016) introduced in response to psychology's own reproducibility crisis. To efficiently explore high-dimensional and often continuous ML search spaces, we model the multiverse with a Gaussian Process surrogate and apply Bayesian experimental design. Our framework is designed to facilitate drawing robust scientific conclusions about model performance, and thus our approach focuses on exploration rather than conventional optimization. In the first of two case studies, we investigate disputed claims about the relative merit of adaptive optimizers. Second, we synthesize conflicting research on the effect of learning rate on the large batch training generalization gap. For the machine learning community, the Multiverse Analysis is a simple and effective technique for identifying robust claims, for increasing transparency, and a step toward improved reproducibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge