Model-free prediction of spatiotemporal dynamical systems with recurrent neural networks: Role of network spectral radius
Paper and Code
Oct 10, 2019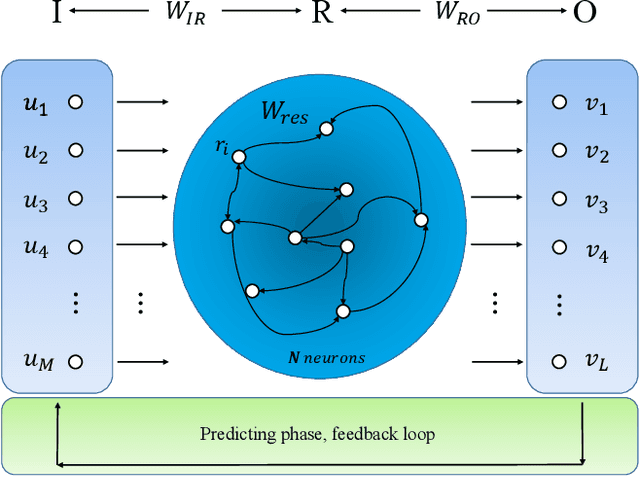
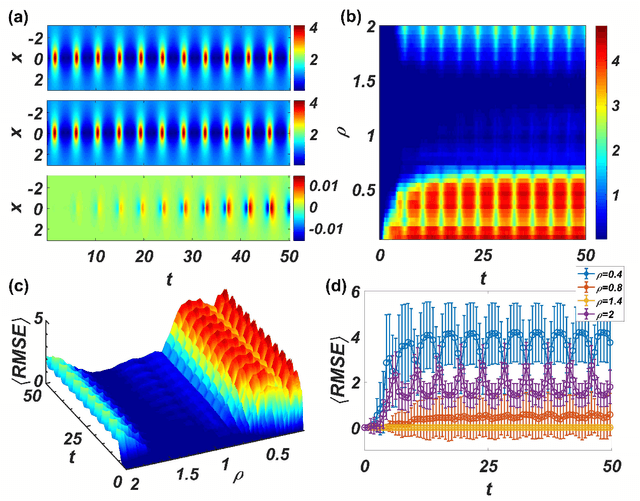
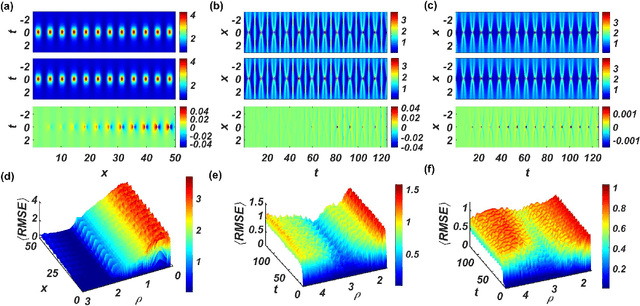
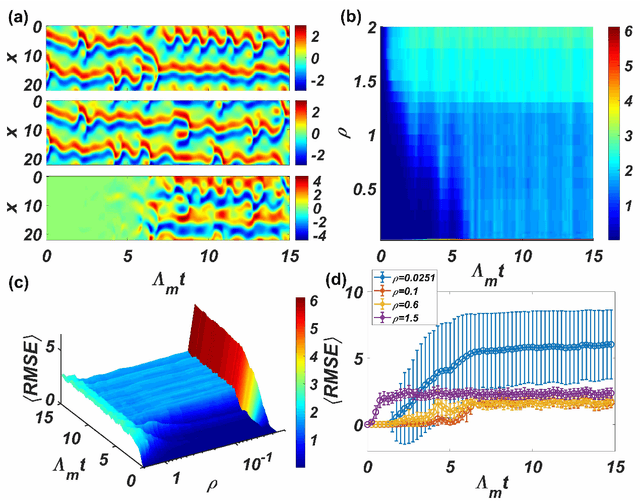
A common difficulty in applications of machine learning is the lack of any general principle for guiding the choices of key parameters of the underlying neural network. Focusing on a class of recurrent neural networks - reservoir computing systems that have recently been exploited for model-free prediction of nonlinear dynamical systems, we uncover a surprising phenomenon: the emergence of an interval in the spectral radius of the neural network in which the prediction error is minimized. In a three-dimensional representation of the error versus time and spectral radius, the interval corresponds to the bottom region of a "valley." Such a valley arises for a variety of spatiotemporal dynamical systems described by nonlinear partial differential equations, regardless of the structure and the edge-weight distribution of the underlying reservoir network. We also find that, while the particular location and size of the valley would depend on the details of the target system to be predicted, the interval tends to be larger for undirected than for directed networks. The valley phenomenon can be beneficial to the design of optimal reservoir computing, representing a small step forward in understanding these machine-learning systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge