Model Compression for Domain Adaptation through Causal Effect Estimation

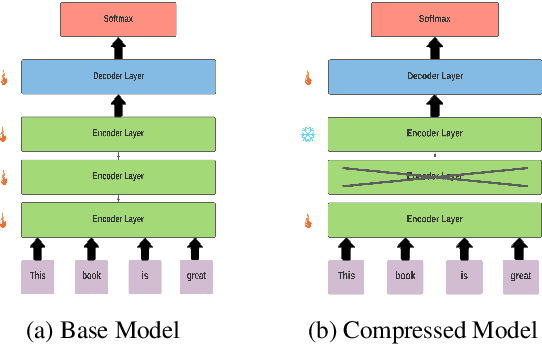
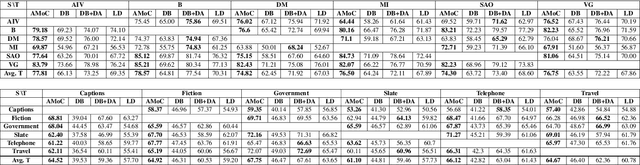
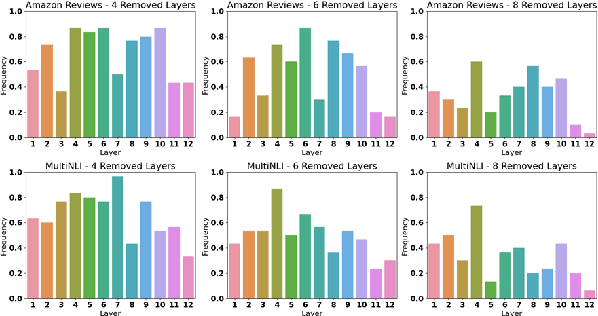
Recent improvements in the predictive quality of natural language processing systems are often dependent on a substantial increase in the number of model parameters. This has led to various attempts of compressing such models, but existing methods have not considered the differences in the predictive power of various model components or in the generalizability of the compressed models. To understand the connection between model compression and out-of-distribution generalization, we define the task of compressing language representation models such that they perform best in a domain adaptation setting. We choose to address this problem from a causal perspective, attempting to estimate the \textit{average treatment effect} (ATE) of a model component, such as a single layer, on the model's predictions. Our proposed ATE-guided Model Compression scheme (AMoC), generates many model candidates, differing by the model components that were removed. Then, we select the best candidate through a stepwise regression model that utilizes the ATE to predict the expected performance on the target domain. AMoC outperforms strong baselines on 46 of 60 domain pairs across two text classification tasks, with an average improvement of more than 3\% in F1 above the strongest baseline.