Model-based recursive partitioning for discrete event times
Paper and Code
Sep 14, 2022

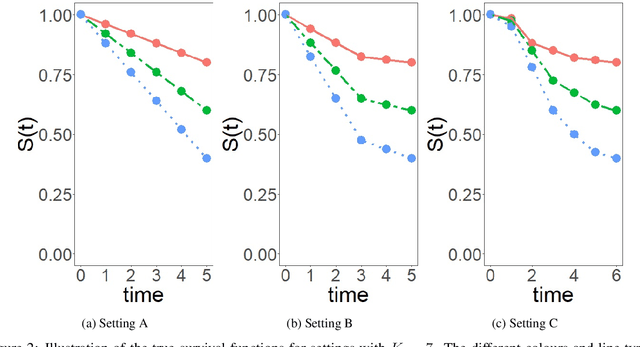
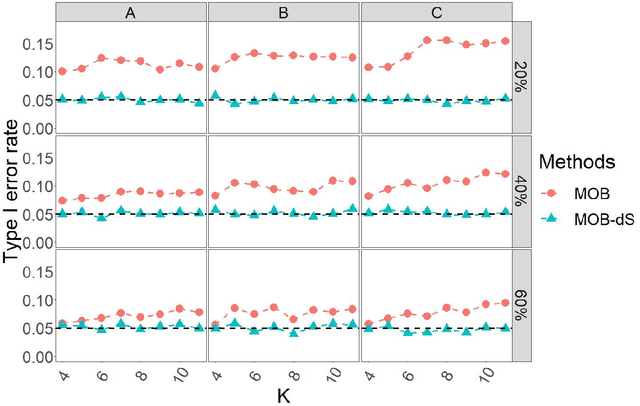
Model-based recursive partitioning (MOB) is a semi-parametric statistical approach allowing the identification of subgroups that can be combined with a broad range of outcome measures including continuous time-to-event outcomes. When time is measured on a discrete scale, methods and models need to account for this discreetness as otherwise subgroups might be spurious and effects biased. The test underlying the splitting criterion of MOB, the M-fluctuation test, assumes independent observations. However, for fitting discrete time-to-event models the data matrix has to be modified resulting in an augmented data matrix violating the independence assumption. We propose MOB for discrete Survival data (MOB-dS) which controls the type I error rate of the test used for data splitting and therefore the rate of identifying subgroups although none is present. MOB-ds uses a permutation approach accounting for dependencies in the augmented time-to-event data to obtain the distribution under the null hypothesis of no subgroups being present. Through simulations we investigate the type I error rate of the new MOB-dS and the standard MOB for different patterns of survival curves and event rates. We find that the type I error rates of the test is well controlled for MOB-dS, but observe some considerable inflations of the error rate for MOB. To illustrate the proposed methods, MOB-dS is applied to data on unemployment duration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge