Mode Connectivity and Data Heterogeneity of Federated Learning
Paper and Code
Sep 29, 2023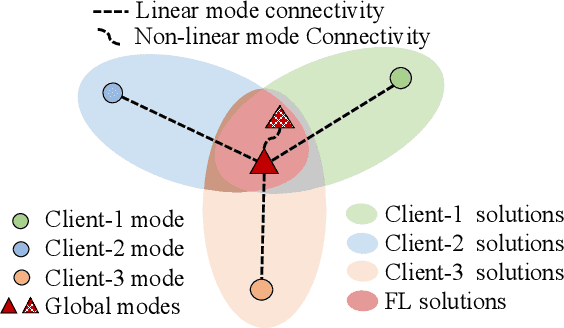
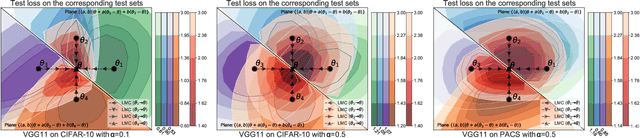
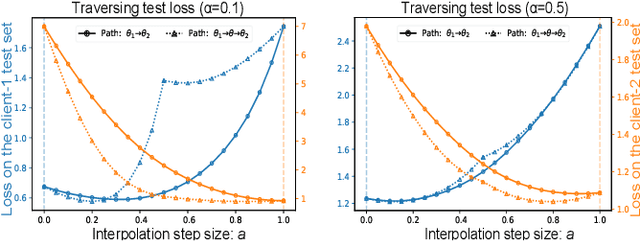
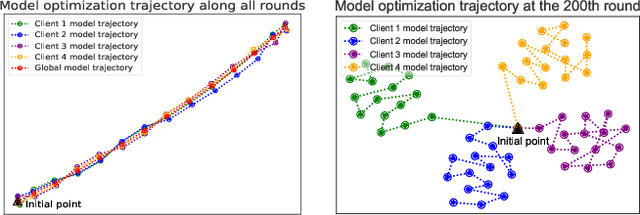
Federated learning (FL) enables multiple clients to train a model while keeping their data private collaboratively. Previous studies have shown that data heterogeneity between clients leads to drifts across client updates. However, there are few studies on the relationship between client and global modes, making it unclear where these updates end up drifting. We perform empirical and theoretical studies on this relationship by utilizing mode connectivity, which measures performance change (i.e., connectivity) along parametric paths between different modes. Empirically, reducing data heterogeneity makes the connectivity on different paths more similar, forming more low-error overlaps between client and global modes. We also find that a barrier to connectivity occurs when linearly connecting two global modes, while it disappears with considering non-linear mode connectivity. Theoretically, we establish a quantitative bound on the global-mode connectivity using mean-field theory or dropout stability. The bound demonstrates that the connectivity improves when reducing data heterogeneity and widening trained models. Numerical results further corroborate our analytical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge