Möbius Convolutions for Spherical CNNs

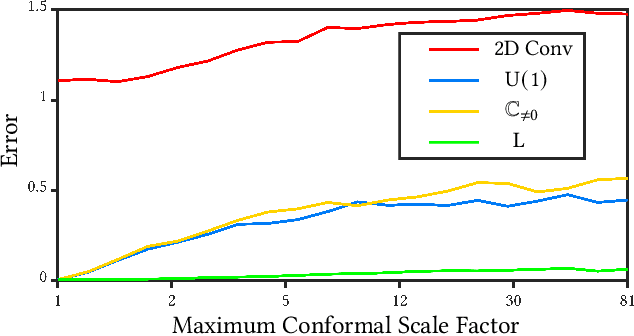
M\"{o}bius transformations play an important role in both geometry and spherical image processing -- they are the group of conformal automorphisms of 2D surfaces and the spherical equivalent of homographies. Here we present a novel, M\"{o}bius-equivariant spherical convolution operator which we call M\"{o}bius convolution, and with it, develop the foundations for M\"{o}bius-equivariant spherical CNNs. Our approach is based on a simple observation: to achieve equivariance, we only need to consider the lower-dimensional subgroup which transforms the positions of points as seen in the frames of their neighbors. To efficiently compute M\"{o}bius convolutions at scale we derive an approximation of the action of the transformations on spherical filters, allowing us to compute our convolutions in the spectral domain with the fast Spherical Harmonic Transform. The resulting framework is both flexible and descriptive, and we demonstrate its utility by achieving promising results in both shape classification and image segmentation tasks.