MLPnP - A Real-Time Maximum Likelihood Solution to the Perspective-n-Point Problem
Paper and Code
Jul 27, 2016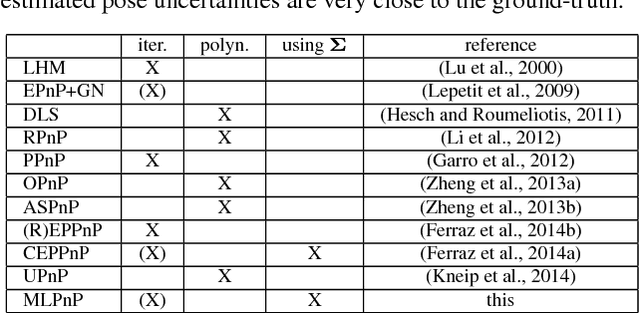
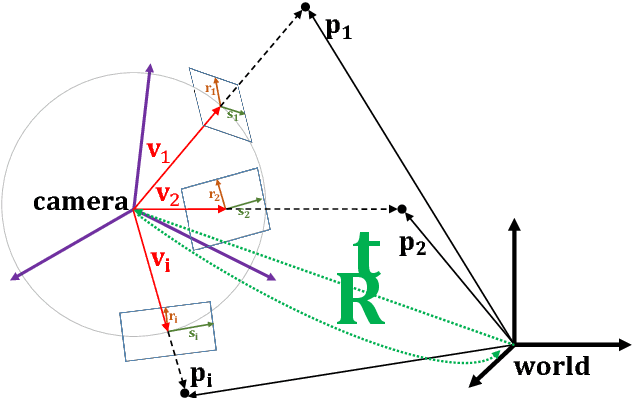
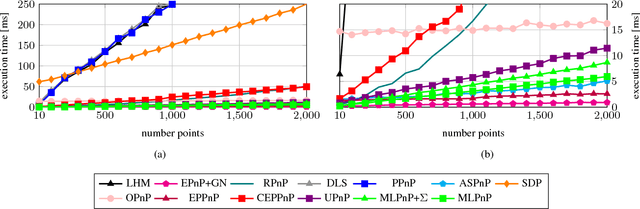

In this paper, a statistically optimal solution to the Perspective-n-Point (PnP) problem is presented. Many solutions to the PnP problem are geometrically optimal, but do not consider the uncertainties of the observations. In addition, it would be desirable to have an internal estimation of the accuracy of the estimated rotation and translation parameters of the camera pose. Thus, we propose a novel maximum likelihood solution to the PnP problem, that incorporates image observation uncertainties and remains real-time capable at the same time. Further, the presented method is general, as is works with 3D direction vectors instead of 2D image points and is thus able to cope with arbitrary central camera models. This is achieved by projecting (and thus reducing) the covariance matrices of the observations to the corresponding vector tangent space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge