Mixed Logit Models and Network Formation

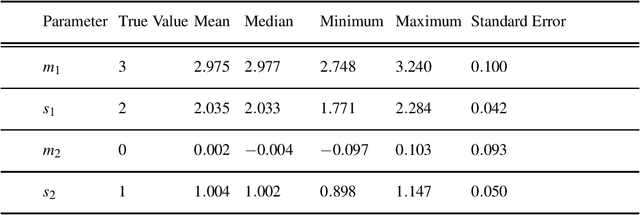
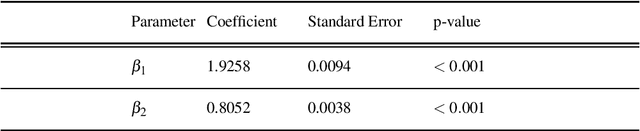
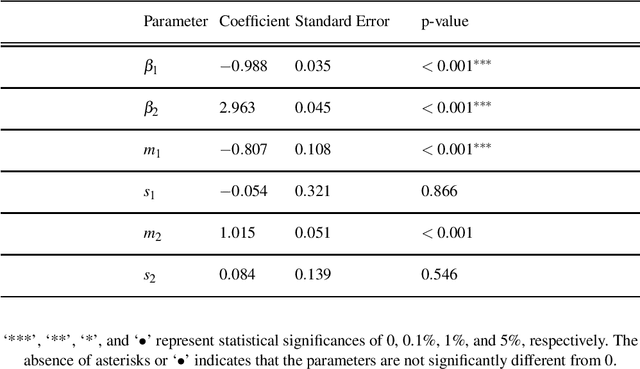
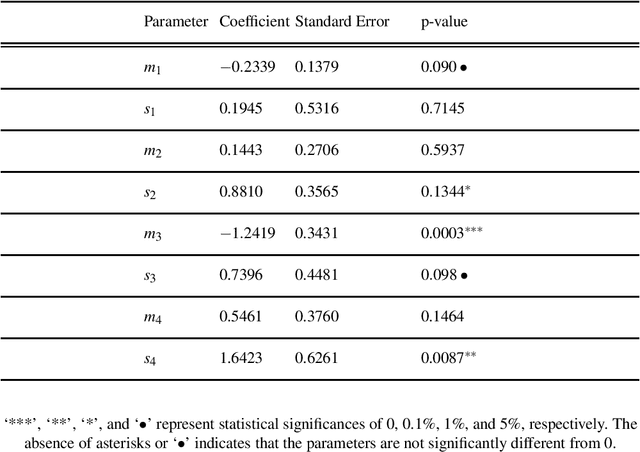
The study of network formation is pervasive in economics, sociology, and many other fields. In this paper, we model network formation as a ``choice'' that is made by nodes in a network to connect to other nodes. We study these ``choices'' using discrete-choice models, in which an agent chooses between two or more discrete alternatives. One framework for studying network formation is the multinomial logit (MNL) model. We highlight limitations of the MNL model on networks that are constructed from empirical data. We employ the ``repeated choice'' (RC) model to study network formation \cite{TrainRevelt97mixedlogit}. We argue that the RC model overcomes important limitations of the MNL model and is well-suited to study network formation. We also illustrate how to use the RC model to accurately study network formation using both synthetic and real-world networks. Using synthetic networks, we also compare the performance of the MNL model and the RC model; we find that the RC model estimates the data-generation process of our synthetic networks more accurately than the MNL model. We provide examples of qualitatively interesting questions -- the presence of homophily in a teen friendship network and the fact that new patents are more likely to cite older, more cited, and similar patents -- for which the RC model allows us to achieve insights.