Mitigating multiple descents: A model-agnostic framework for risk monotonization
Paper and Code
May 25, 2022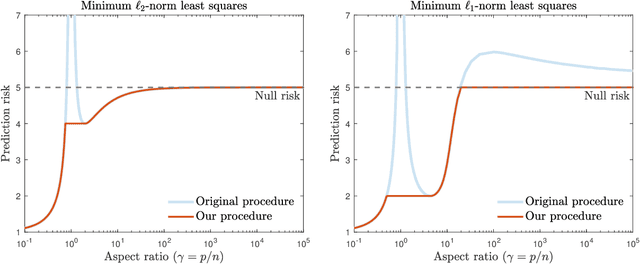

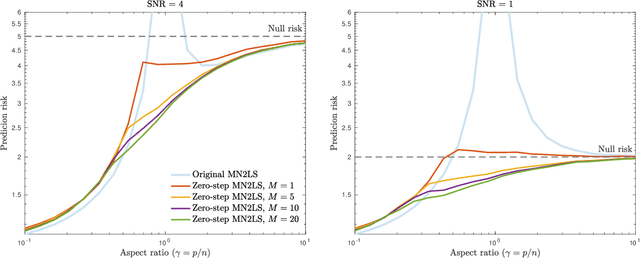

Recent empirical and theoretical analyses of several commonly used prediction procedures reveal a peculiar risk behavior in high dimensions, referred to as double/multiple descent, in which the asymptotic risk is a non-monotonic function of the limiting aspect ratio of the number of features or parameters to the sample size. To mitigate this undesirable behavior, we develop a general framework for risk monotonization based on cross-validation that takes as input a generic prediction procedure and returns a modified procedure whose out-of-sample prediction risk is, asymptotically, monotonic in the limiting aspect ratio. As part of our framework, we propose two data-driven methodologies, namely zero- and one-step, that are akin to bagging and boosting, respectively, and show that, under very mild assumptions, they provably achieve monotonic asymptotic risk behavior. Our results are applicable to a broad variety of prediction procedures and loss functions, and do not require a well-specified (parametric) model. We exemplify our framework with concrete analyses of the minimum $\ell_2$, $\ell_1$-norm least squares prediction procedures. As one of the ingredients in our analysis, we also derive novel additive and multiplicative forms of oracle risk inequalities for split cross-validation that are of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge