Mining Large Quasi-cliques with Quality Guarantees from Vertex Neighborhoods
Paper and Code
Aug 18, 2020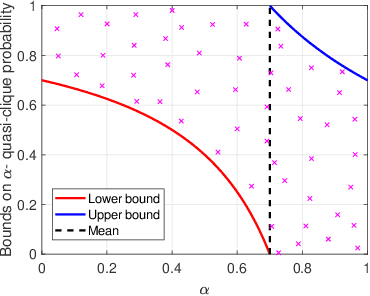
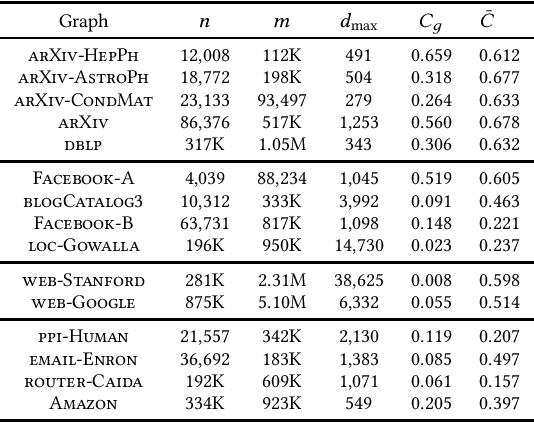
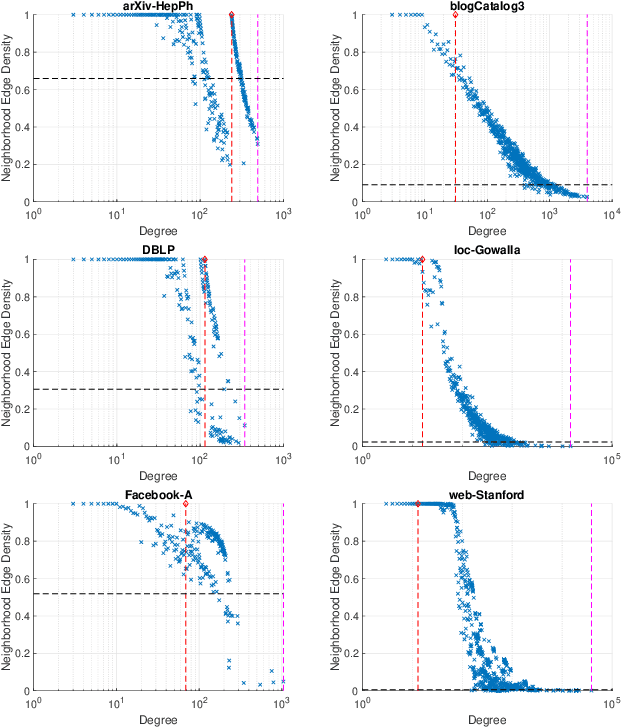
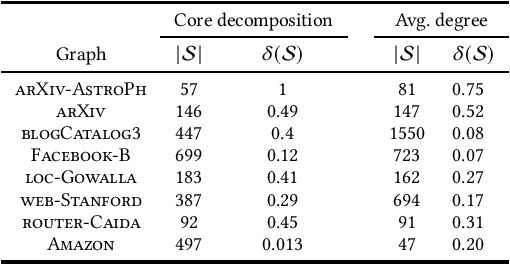
Mining dense subgraphs is an important primitive across a spectrum of graph-mining tasks. In this work, we formally establish that two recurring characteristics of real-world graphs, namely heavy-tailed degree distributions and large clustering coefficients, imply the existence of substantially large vertex neighborhoods with high edge-density. This observation suggests a very simple approach for extracting large quasi-cliques: simply scan the vertex neighborhoods, compute the clustering coefficient of each vertex, and output the best such subgraph. The implementation of such a method requires counting the triangles in a graph, which is a well-studied problem in graph mining. When empirically tested across a number of real-world graphs, this approach reveals a surprise: vertex neighborhoods include maximal cliques of non-trivial sizes, and the density of the best neighborhood often compares favorably to subgraphs produced by dedicated algorithms for maximizing subgraph density. For graphs with small clustering coefficients, we demonstrate that small vertex neighborhoods can be refined using a local-search method to ``grow'' larger cliques and near-cliques. Our results indicate that contrary to worst-case theoretical results, mining cliques and quasi-cliques of non-trivial sizes from real-world graphs is often not a difficult problem, and provides motivation for further work geared towards a better explanation of these empirical successes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge