Minimum Description Length Control

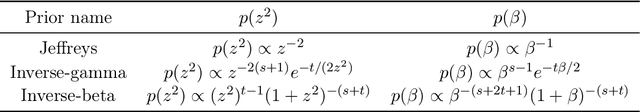
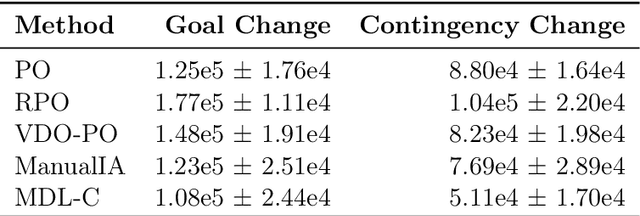
We propose a novel framework for multitask reinforcement learning based on the minimum description length (MDL) principle. In this approach, which we term MDL-control (MDL-C), the agent learns the common structure among the tasks with which it is faced and then distills it into a simpler representation which facilitates faster convergence and generalization to new tasks. In doing so, MDL-C naturally balances adaptation to each task with epistemic uncertainty about the task distribution. We motivate MDL-C via formal connections between the MDL principle and Bayesian inference, derive theoretical performance guarantees, and demonstrate MDL-C's empirical effectiveness on both discrete and high-dimensional continuous control tasks.