Minimizing the Expected Posterior Entropy Yields Optimal Summary Statistics
Paper and Code
Jun 06, 2022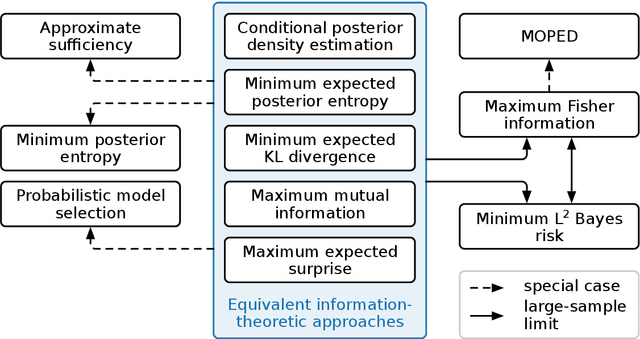
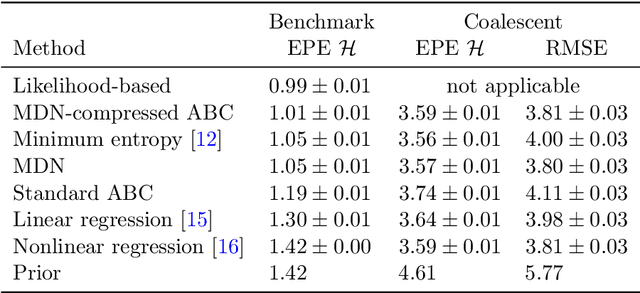
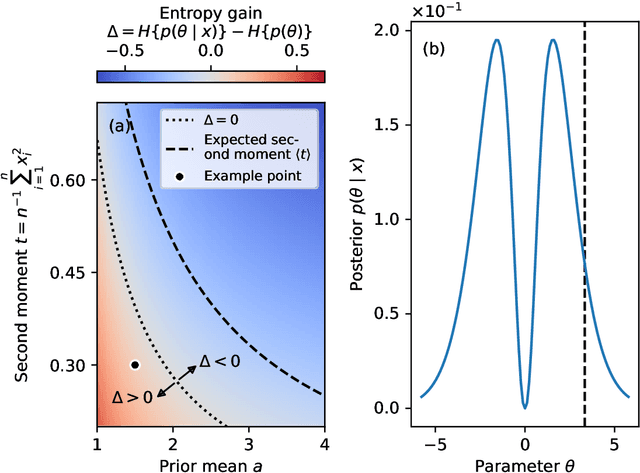

Extracting low-dimensional summary statistics from large datasets is essential for efficient (likelihood-free) inference. We propose obtaining summary statistics by minimizing the expected posterior entropy (EPE) under the prior predictive distribution of the model. We show that minimizing the EPE is equivalent to learning a conditional density estimator for the posterior as well as other information-theoretic approaches. Further summary extraction methods (including minimizing the $L^2$ Bayes risk, maximizing the Fisher information, and model selection approaches) are special or limiting cases of EPE minimization. We demonstrate that the approach yields high fidelity summary statistics by applying it to both a synthetic benchmark as well as a population genetics problem. We not only offer concrete recommendations for practitioners but also provide a unifying perspective for obtaining informative summary statistics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge