Minimax Policy for Heavy-tailed Multi-armed Bandits
Paper and Code
Jul 20, 2020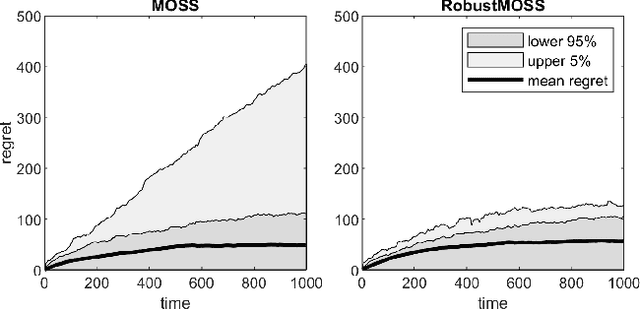
We study the stochastic Multi-Armed Bandit (MAB) problem under worst case regret and heavy-tailed reward distribution. We modify the minimax policy MOSS~\cite{MOSS} for the sub-Gaussian reward distribution by using saturated empirical mean to design a new algorithm called Robust MOSS. We show that if the moment of order $1+\epsilon$ for the reward distribution exists, then the refined strategy has a worst-case regret matching the lower bound while maintaining a distribution dependent logarithm regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge