Metatrace: Online Step-size Tuning by Meta-gradient Descent for Reinforcement Learning Control

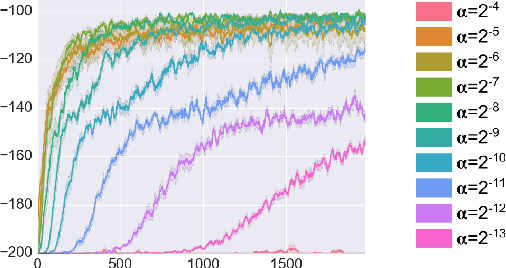
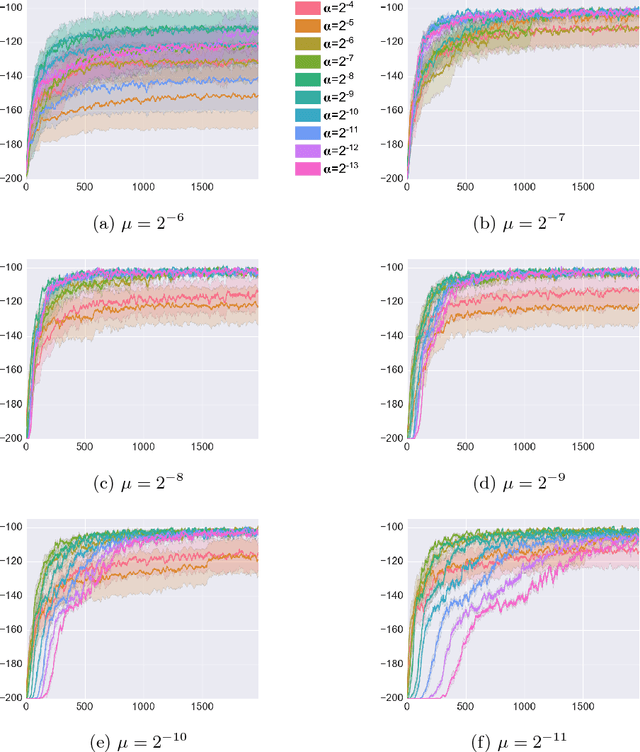
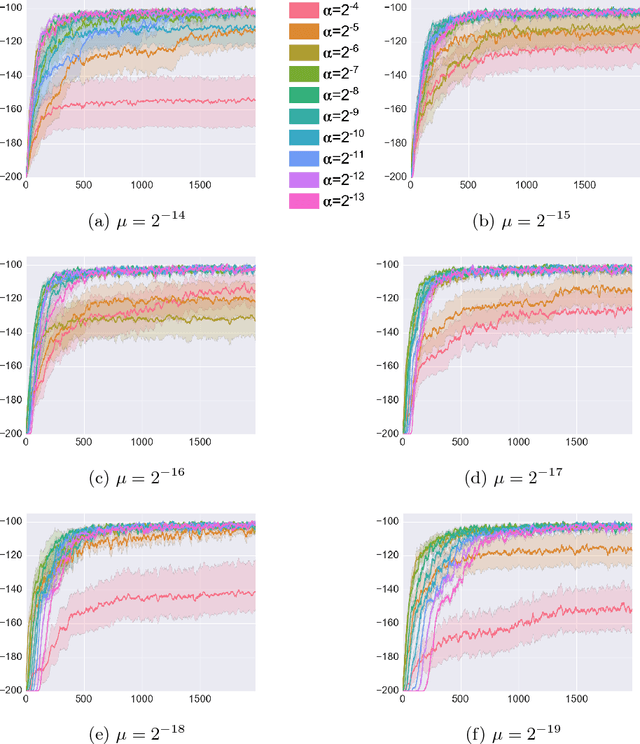
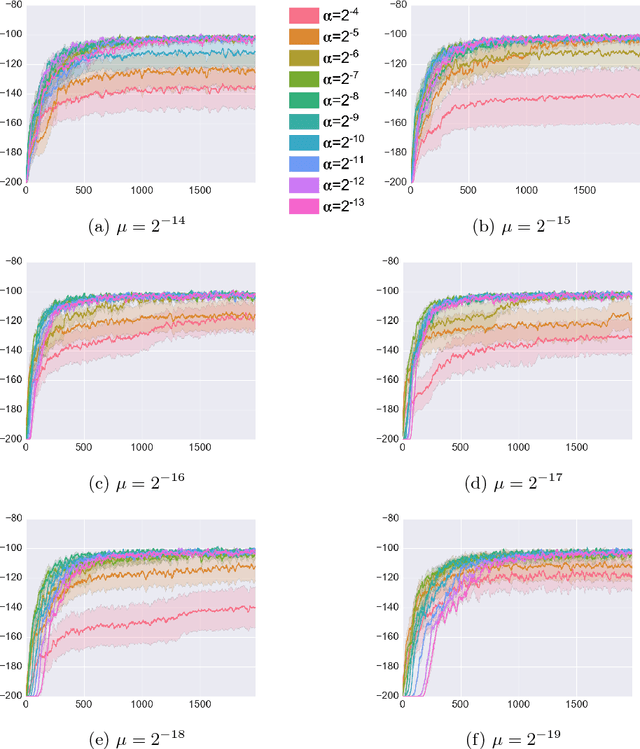
Reinforcement learning (RL) has had many successes in both "deep" and "shallow" settings. In both cases, significant hyperparameter tuning is often required to achieve good performance. Furthermore, when nonlinear function approximation is used, non-stationarity in the state representation can lead to learning instability. A variety of techniques exist to combat this --- most notably large experience replay buffers or the use of multiple parallel actors. These techniques come at the cost of moving away from the online RL problem as it is traditionally formulated (i.e., a single agent learning online without maintaining a large database of training examples). Meta-learning can potentially help with both these issues by tuning hyperparameters online and allowing the algorithm to more robustly adjust to non-stationarity in a problem. This paper applies meta-gradient descent to derive a set of step-size tuning algorithms specifically for online RL control with eligibility traces. Our novel technique, Metatrace, makes use of an eligibility trace analogous to methods like $TD(\lambda)$. We explore tuning both a single scalar step-size and a separate step-size for each learned parameter. We evaluate Metatrace first for control with linear function approximation in the classic mountain car problem and then in a noisy, non-stationary version. Finally, we apply Metatrace for control with nonlinear function approximation in 5 games in the Arcade Learning Environment where we explore how it impacts learning speed and robustness to initial step-size choice. Results show that the meta-step-size parameter of Metatrace is easy to set, Metatrace can speed learning, and Metatrace can allow an RL algorithm to deal with non-stationarity in the learning task.