Meta-Learning Online Control for Linear Dynamical Systems
Paper and Code
Aug 18, 2022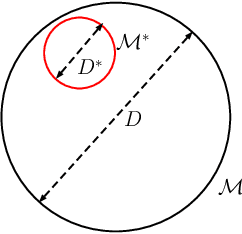
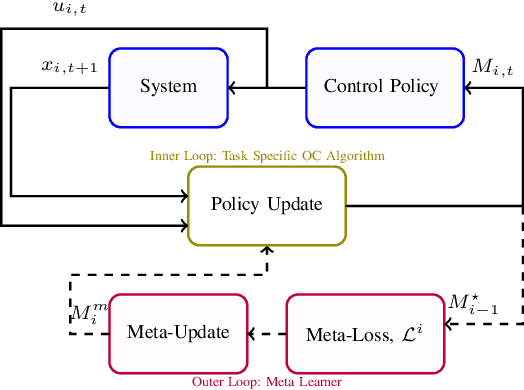
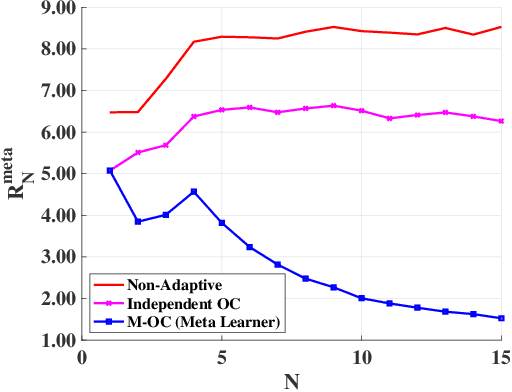
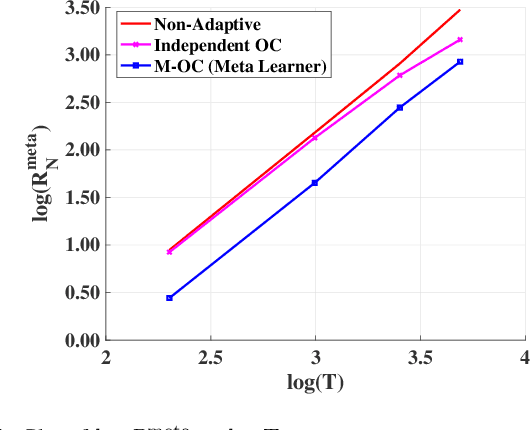
In this paper, we consider the problem of finding a meta-learning online control algorithm that can learn across the tasks when faced with a sequence of $N$ (similar) control tasks. Each task involves controlling a linear dynamical system for a finite horizon of $T$ time steps. The cost function and system noise at each time step are adversarial and unknown to the controller before taking the control action. Meta-learning is a broad approach where the goal is to prescribe an online policy for any new unseen task exploiting the information from other tasks and the similarity between the tasks. We propose a meta-learning online control algorithm for the control setting and characterize its performance by \textit{meta-regret}, the average cumulative regret across the tasks. We show that when the number of tasks are sufficiently large, our proposed approach achieves a meta-regret that is smaller by a factor $D/D^{*}$ compared to an independent-learning online control algorithm which does not perform learning across the tasks, where $D$ is a problem constant and $D^{*}$ is a scalar that decreases with increase in the similarity between tasks. Thus, when the sequence of tasks are similar the regret of the proposed meta-learning online control is significantly lower than that of the naive approaches without meta-learning. We also present experiment results to demonstrate the superior performance achieved by our meta-learning algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge