Mean Field Analysis of Deep Neural Networks

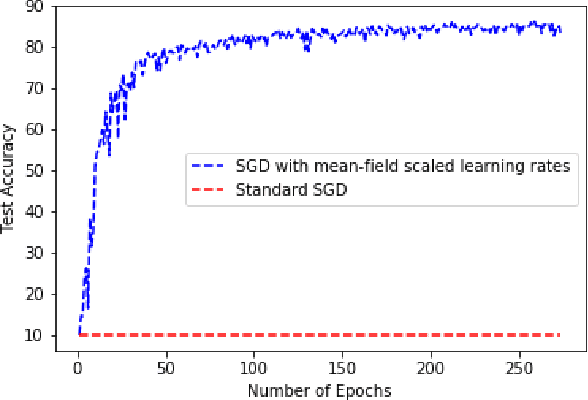
We analyze multi-layer neural networks in the asymptotic regime of simultaneously (A) large network sizes and (B) large numbers of stochastic gradient descent training iterations. We rigorously establish the limiting behavior of the multilayer neural network output. The limit procedure is valid for any number of hidden layers and it naturally also describes the limiting behavior of the training loss. The ideas that we explore are to (a) sequentially take the limits of each hidden layer and (b) characterizing the evolution of parameters in terms of their initialization. The limit satisfies a system of integro-differential equations.