MDPFuzzer: Finding Crash-Triggering State Sequences in Models Solving the Markov Decision Process

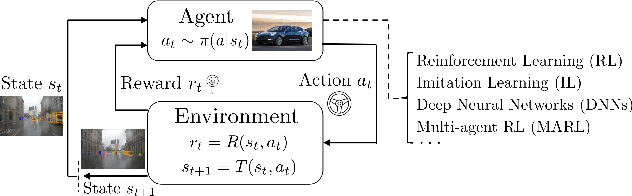
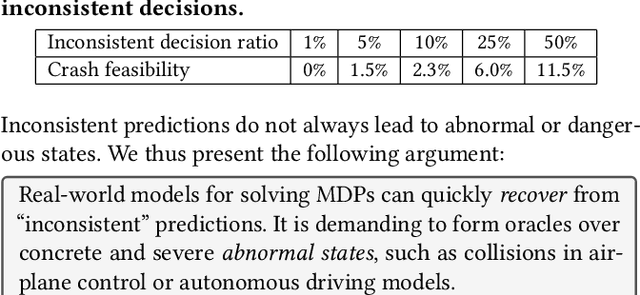
The Markov decision process (MDP) provides a mathematical framework for modeling sequential decision-making problems, many of which are crucial to security and safety, such as autonomous driving and robot control. The rapid development of artificial intelligence research has created efficient methods for solving MDPs, such as deep neural networks (DNNs), reinforcement learning (RL), and imitation learning (IL). However, these popular models for solving MDPs are neither thoroughly tested nor rigorously reliable. We present MDPFuzzer, the first blackbox fuzz testing framework for models solving MDPs. MDPFuzzer forms testing oracles by checking whether the target model enters abnormal and dangerous states. During fuzzing, MDPFuzzer decides which mutated state to retain by measuring if it can reduce cumulative rewards or form a new state sequence. We design efficient techniques to quantify the "freshness" of a state sequence using Gaussian mixture models (GMMs) and dynamic expectation-maximization (DynEM). We also prioritize states with high potential of revealing crashes by estimating the local sensitivity of target models over states. MDPFuzzer is evaluated on five state-of-the-art models for solving MDPs, including supervised DNN, RL, IL, and multi-agent RL. Our evaluation includes scenarios of autonomous driving, aircraft collision avoidance, and two games that are often used to benchmark RL. During a 12-hour run, we find over 80 crash-triggering state sequences on each model. We show inspiring findings that crash-triggering states, though look normal, induce distinct neuron activation patterns compared with normal states. We further develop an abnormal behavior detector to harden all the evaluated models and repair them with the findings of MDPFuzzer to significantly enhance their robustness without sacrificing accuracy.