May the Noise be with you: Adversarial Training without Adversarial Examples
Paper and Code
Dec 12, 2023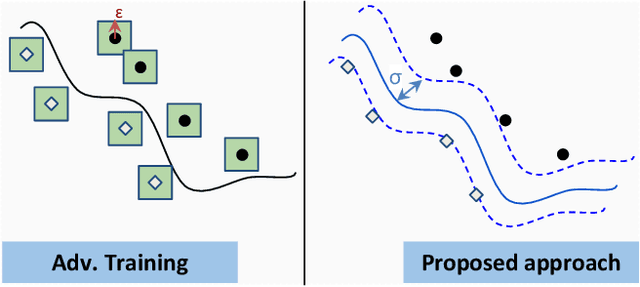
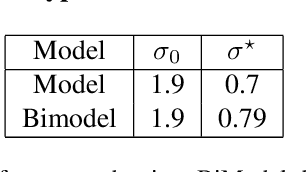
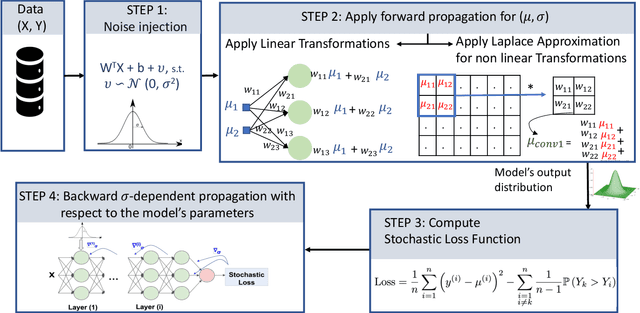
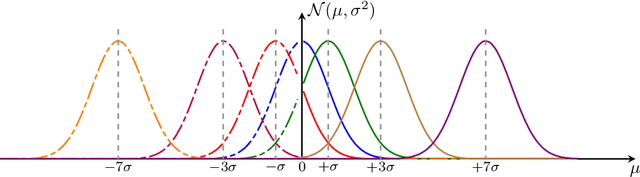
In this paper, we investigate the following question: Can we obtain adversarially-trained models without training on adversarial examples? Our intuition is that training a model with inherent stochasticity, i.e., optimizing the parameters by minimizing a stochastic loss function, yields a robust expectation function that is non-stochastic. In contrast to related methods that introduce noise at the input level, our proposed approach incorporates inherent stochasticity by embedding Gaussian noise within the layers of the NN model at training time. We model the propagation of noise through the layers, introducing a closed-form stochastic loss function that encapsulates a noise variance parameter. Additionally, we contribute a formalized noise-aware gradient, enabling the optimization of model parameters while accounting for stochasticity. Our experimental results confirm that the expectation model of a stochastic architecture trained on benign distribution is adversarially robust. Interestingly, we find that the impact of the applied Gaussian noise's standard deviation on both robustness and baseline accuracy closely mirrors the impact of the noise magnitude employed in adversarial training. Our work contributes adversarially trained networks using a completely different approach, with empirically similar robustness to adversarial training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge