Maximum Likelihood Methods for Inverse Learning of Optimal Controllers
Paper and Code
May 06, 2020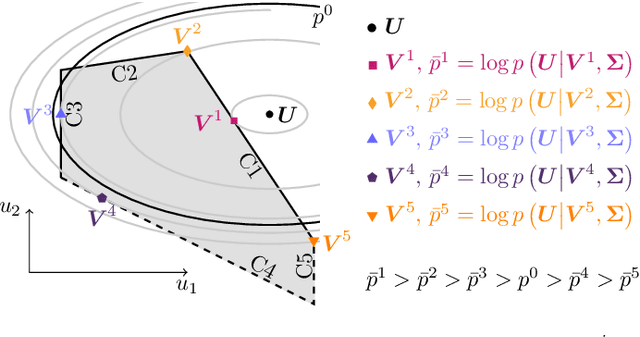


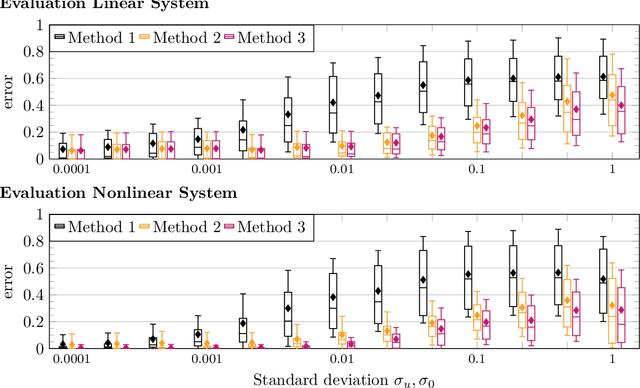
This paper presents a framework for inverse learning of objective functions for constrained optimal control problems, which is based on the Karush-Kuhn-Tucker (KKT) conditions. We discuss three variants corresponding to different model assumptions and computational complexities. The first method uses a convex relaxation of the KKT conditions and serves as the benchmark. The main contribution of this paper is the proposition of two learning methods that combine the KKT conditions with maximum likelihood estimation. The key benefit of this combination is the systematic treatment of constraints for learning from noisy data with a branch-and-bound algorithm using likelihood arguments. This paper discusses theoretic properties of the learning methods and presents simulation results that highlight the advantages of using the maximum likelihood formulation for learning objective functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge