Maximum Likelihood Constraint Inference for Inverse Reinforcement Learning

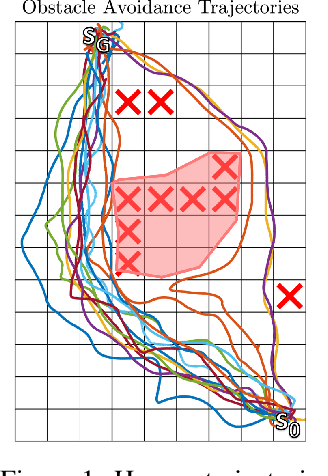
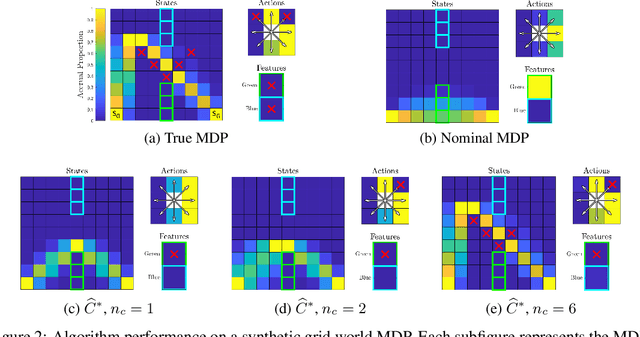
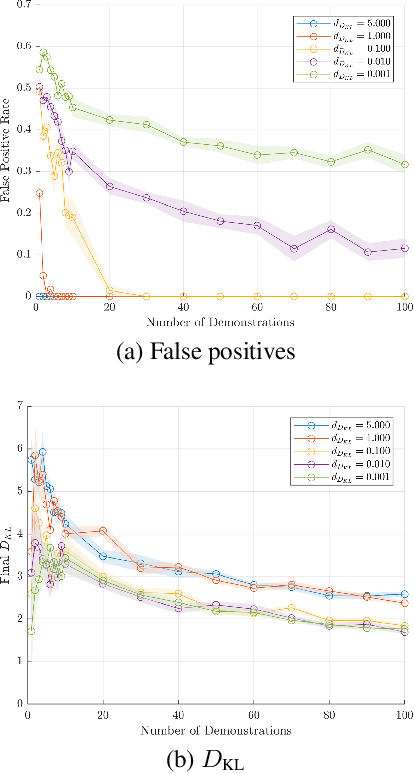
While most approaches to the problem of Inverse Reinforcement Learning (IRL) focus on estimating a reward function that best explains an expert agent's policy or demonstrated behavior on a control task, it is often the case that such behavior is more succinctly described by a simple reward combined with a set of hard constraints. In this setting, the agent is attempting to maximize cumulative rewards subject to these given constraints on their behavior. We reformulate the problem of IRL on Markov Decision Processes (MDPs) such that, given a nominal model of the environment and a nominal reward function, we seek to estimate state, action, and feature constraints in the environment that motivate an agent's behavior. Our approach is based on the Maximum Entropy IRL framework, which allows us to reason about the likelihood of an expert agent's demonstrations given our knowledge of an MDP. Using our method, we can infer which constraints can be added to the MDP to most increase the likelihood of observing these demonstrations. We present an algorithm which iteratively infers the Maximum Likelihood Constraint to best explain observed behavior, and we evaluate its efficacy using both simulated behavior and recorded data of humans navigating around an obstacle.