Matrix Difference in Pose-Graph Optimization
Paper and Code
Sep 04, 2018
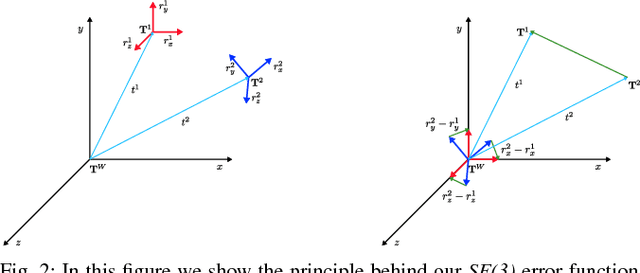

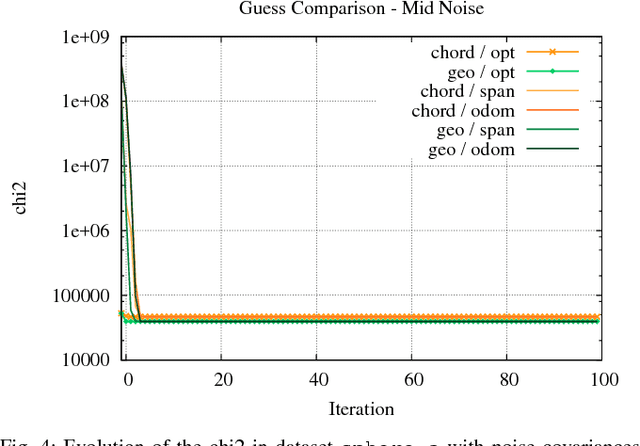
Pose-Graph optimization is a crucial component of many modern SLAM systems. Most prominent state of the art systems address this problem by iterative non-linear least squares. Both number of iterations and convergence basin of these approaches depend on the error functions used to describe the problem. The smoother and more convex the error function with respect to perturbations of the state variables, the better the least-squares solver will perform. In this paper we propose an alternative error function obtained by removing some non-linearities from the standard used one - i.e. the geodesic error function. Comparative experiments conducted on common benchmarking datasets confirm that our function is more robust to noise that affects the rotational component of the pose measurements and, thus, exhibits a larger convergence basin than the geodesic. Furthermore, its implementation is relatively easy compared to the geodesic distance. This property leads to rather simple derivatives and nice numerical properties of the Jacobians resulting from the effective computation of the quadratic approximation used by Gauss-Newton algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge