Masking Strategies for Image Manifolds
Paper and Code
Jun 15, 2016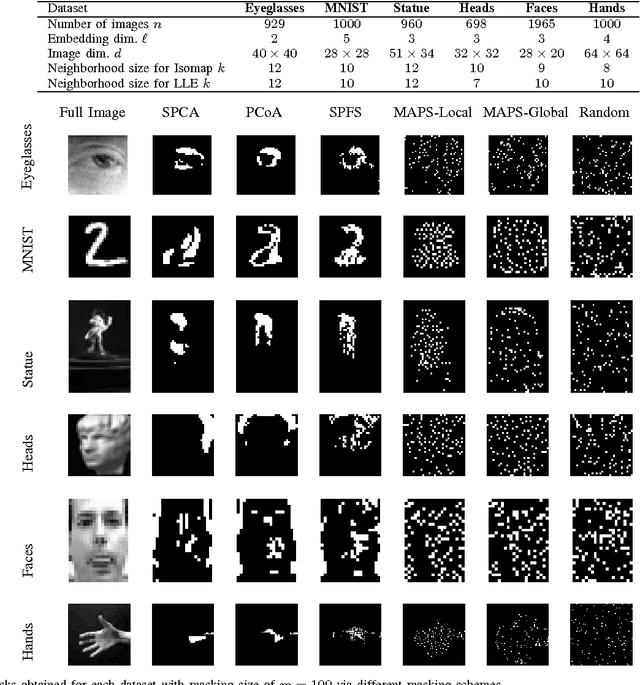
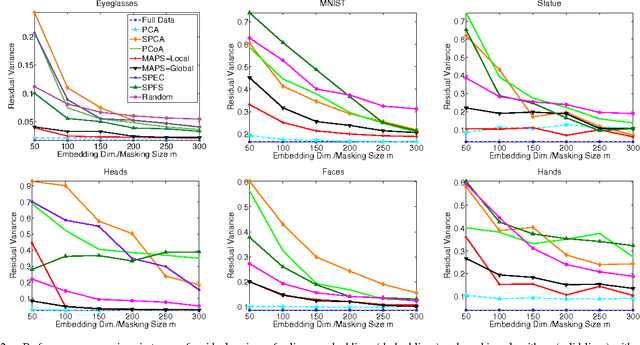
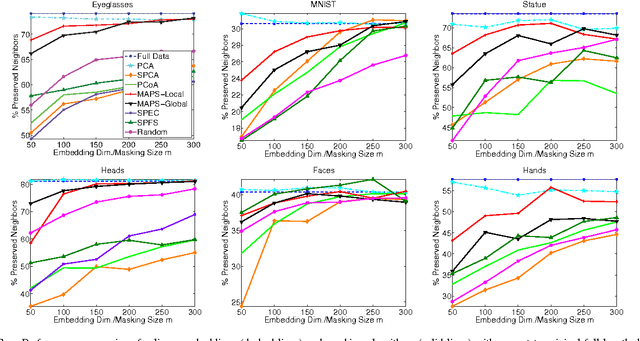
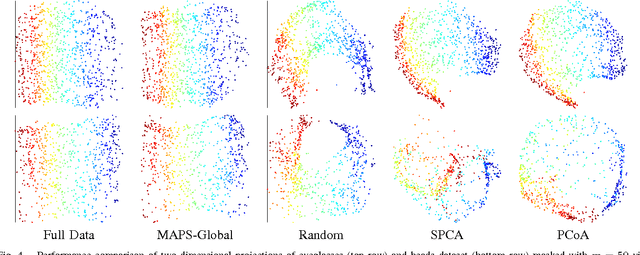
We consider the problem of selecting an optimal mask for an image manifold, i.e., choosing a subset of the pixels of the image that preserves the manifold's geometric structure present in the original data. Such masking implements a form of compressive sensing through emerging imaging sensor platforms for which the power expense grows with the number of pixels acquired. Our goal is for the manifold learned from masked images to resemble its full image counterpart as closely as possible. More precisely, we show that one can indeed accurately learn an image manifold without having to consider a large majority of the image pixels. In doing so, we consider two masking methods that preserve the local and global geometric structure of the manifold, respectively. In each case, the process of finding the optimal masking pattern can be cast as a binary integer program, which is computationally expensive but can be approximated by a fast greedy algorithm. Numerical experiments show that the relevant manifold structure is preserved through the data-dependent masking process, even for modest mask sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge