Manifold Regularization for Adversarial Robustness
Paper and Code
Mar 09, 2020

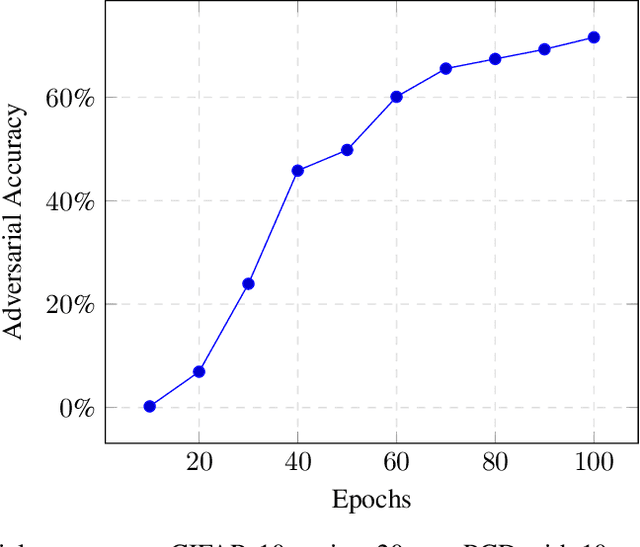
Manifold regularization is a technique that penalizes the complexity of learned functions over the intrinsic geometry of input data. We develop a connection to learning functions which are "locally stable", and propose new regularization terms for training deep neural networks that are stable against a class of local perturbations. These regularizers enable us to train a network to state-of-the-art robust accuracy of 70% on CIFAR-10 against a PGD adversary using $\ell_\infty$ perturbations of size $\epsilon = 8/255$. Furthermore, our techniques do not rely on the construction of any adversarial examples, thus running orders of magnitude faster than standard algorithms for adversarial training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge