Making the Cut: A Bandit-based Approach to Tiered Interviewing

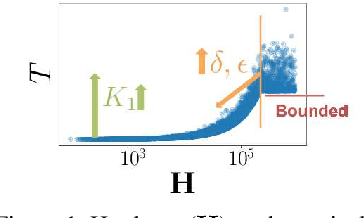
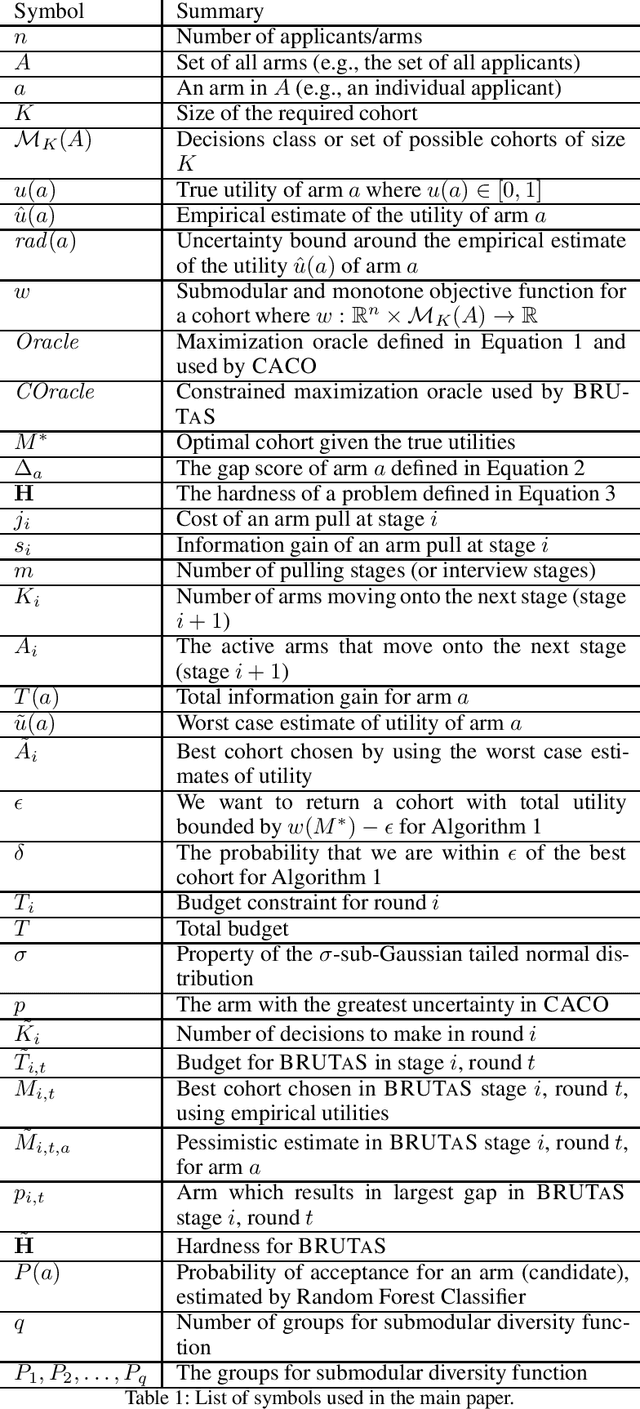
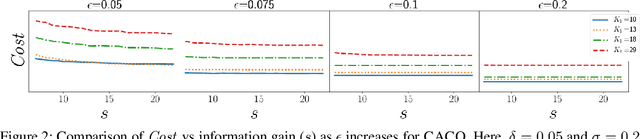
Given a huge set of applicants, how should a firm allocate sequential resume screenings, phone interviews, and in-person site visits? In a tiered interview process, later stages (e.g., in-person visits) are more informative, but also more expensive than earlier stages (e.g., resume screenings). Using accepted hiring models and the concept of structured interviews, a best practice in human resources, we cast tiered hiring as a combinatorial pure exploration (CPE) problem in the stochastic multi-armed bandit setting. The goal is to select a subset of arms (in our case, applicants) with some combinatorial structure. We present new algorithms in both the probably approximately correct (PAC) and fixed-budget settings that select a near-optimal cohort with provable guarantees. We show on real data from one of the largest US-based computer science graduate programs that our algorithms make better hiring decisions or use less budget than the status quo.