Making Linear MDPs Practical via Contrastive Representation Learning
Paper and Code
Jul 14, 2022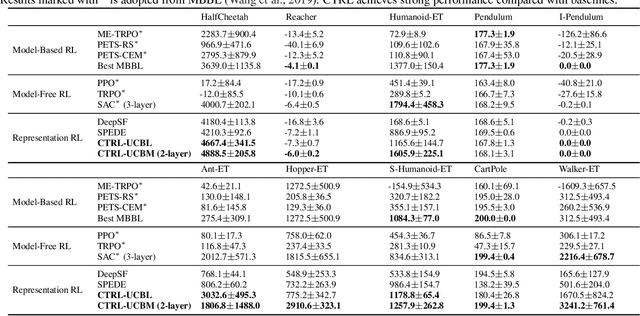
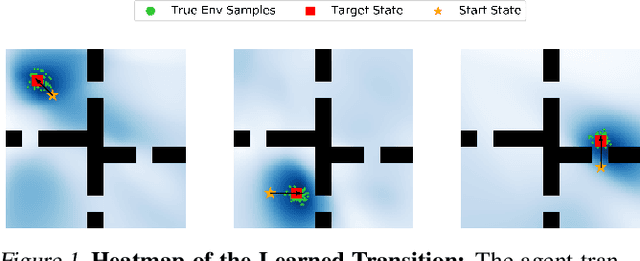


It is common to address the curse of dimensionality in Markov decision processes (MDPs) by exploiting low-rank representations. This motivates much of the recent theoretical study on linear MDPs. However, most approaches require a given representation under unrealistic assumptions about the normalization of the decomposition or introduce unresolved computational challenges in practice. Instead, we consider an alternative definition of linear MDPs that automatically ensures normalization while allowing efficient representation learning via contrastive estimation. The framework also admits confidence-adjusted index algorithms, enabling an efficient and principled approach to incorporating optimism or pessimism in the face of uncertainty. To the best of our knowledge, this provides the first practical representation learning method for linear MDPs that achieves both strong theoretical guarantees and empirical performance. Theoretically, we prove that the proposed algorithm is sample efficient in both the online and offline settings. Empirically, we demonstrate superior performance over existing state-of-the-art model-based and model-free algorithms on several benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge