Machine Learning for SAT: Restricted Heuristics and New Graph Representations
Paper and Code
Jul 18, 2023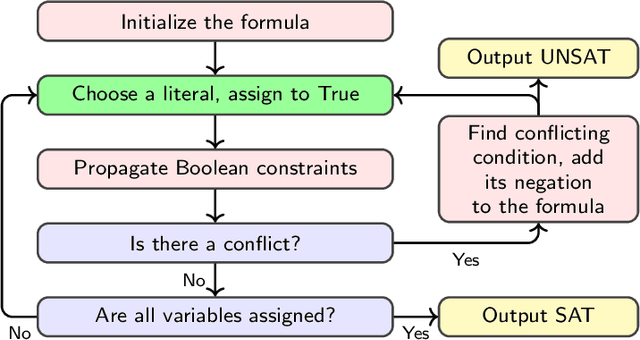
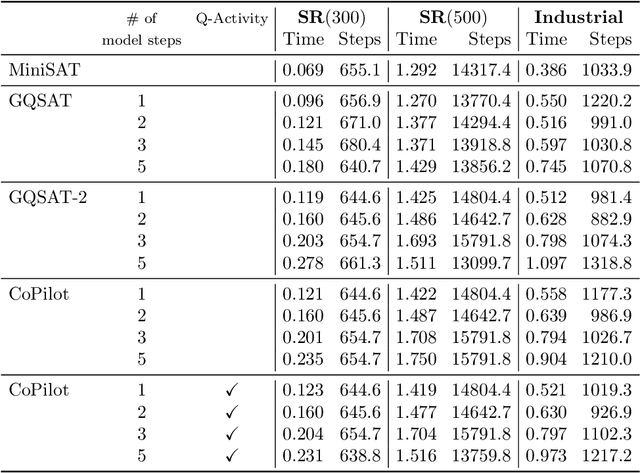
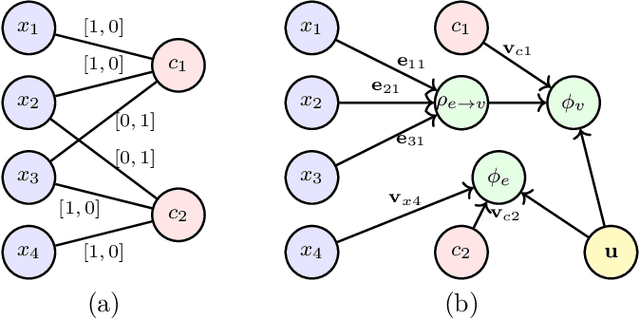
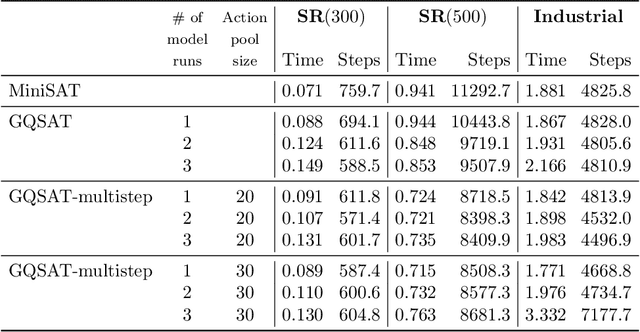
Boolean satisfiability (SAT) is a fundamental NP-complete problem with many applications, including automated planning and scheduling. To solve large instances, SAT solvers have to rely on heuristics, e.g., choosing a branching variable in DPLL and CDCL solvers. Such heuristics can be improved with machine learning (ML) models; they can reduce the number of steps but usually hinder the running time because useful models are relatively large and slow. We suggest the strategy of making a few initial steps with a trained ML model and then releasing control to classical heuristics; this simplifies cold start for SAT solving and can decrease both the number of steps and overall runtime, but requires a separate decision of when to release control to the solver. Moreover, we introduce a modification of Graph-Q-SAT tailored to SAT problems converted from other domains, e.g., open shop scheduling problems. We validate the feasibility of our approach with random and industrial SAT problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge