M-L2O: Towards Generalizable Learning-to-Optimize by Test-Time Fast Self-Adaptation
Paper and Code
Feb 28, 2023
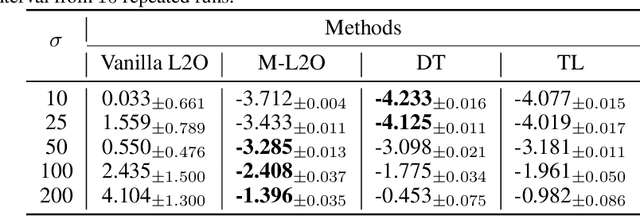


Learning to Optimize (L2O) has drawn increasing attention as it often remarkably accelerates the optimization procedure of complex tasks by ``overfitting" specific task type, leading to enhanced performance compared to analytical optimizers. Generally, L2O develops a parameterized optimization method (i.e., ``optimizer") by learning from solving sample problems. This data-driven procedure yields L2O that can efficiently solve problems similar to those seen in training, that is, drawn from the same ``task distribution". However, such learned optimizers often struggle when new test problems come with a substantially deviation from the training task distribution. This paper investigates a potential solution to this open challenge, by meta-training an L2O optimizer that can perform fast test-time self-adaptation to an out-of-distribution task, in only a few steps. We theoretically characterize the generalization of L2O, and further show that our proposed framework (termed as M-L2O) provably facilitates rapid task adaptation by locating well-adapted initial points for the optimizer weight. Empirical observations on several classic tasks like LASSO and Quadratic, demonstrate that M-L2O converges significantly faster than vanilla L2O with only $5$ steps of adaptation, echoing our theoretical results. Codes are available in https://github.com/VITA-Group/M-L2O.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge