Low Rank Forecasting
Paper and Code
Jan 29, 2021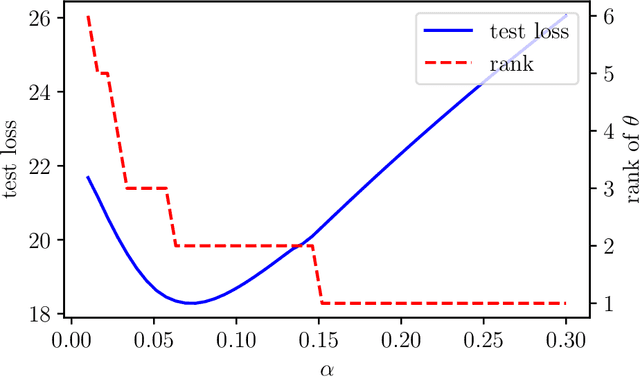
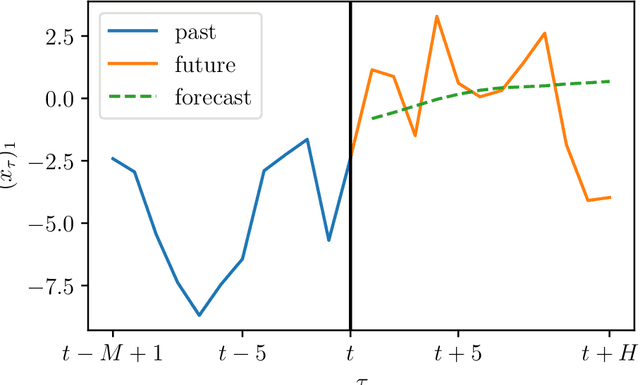
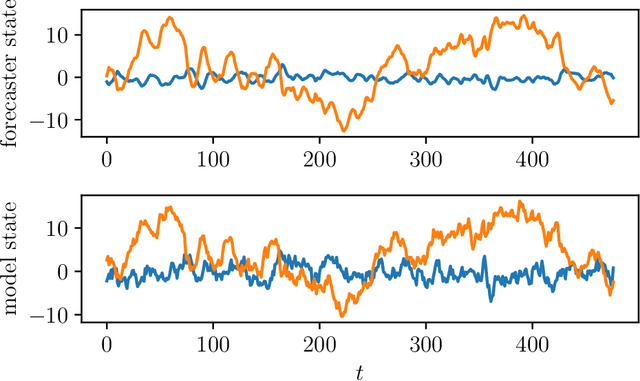
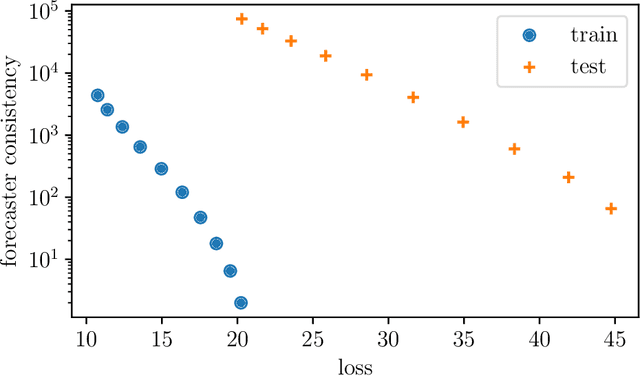
We consider the problem of forecasting multiple values of the future of a vector time series, using some past values. This problem, and related ones such as one-step-ahead prediction, have a very long history, and there are a number of well-known methods for it, including vector auto-regressive models, state-space methods, multi-task regression, and others. Our focus is on low rank forecasters, which break forecasting up into two steps: estimating a vector that can be interpreted as a latent state, given the past, and then estimating the future values of the time series, given the latent state estimate. We introduce the concept of forecast consistency, which means that the estimates of the same value made at different times are consistent. We formulate the forecasting problem in general form, and focus on linear forecasters, for which we propose a formulation that can be solved via convex optimization. We describe a number of extensions and variations, including nonlinear forecasters, data weighting, the inclusion of auxiliary data, and additional objective terms. We illustrate our methods with several examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge