Low-Dose CT Using Denoising Diffusion Probabilistic Model for 20$\times$ Speedup
Paper and Code
Sep 29, 2022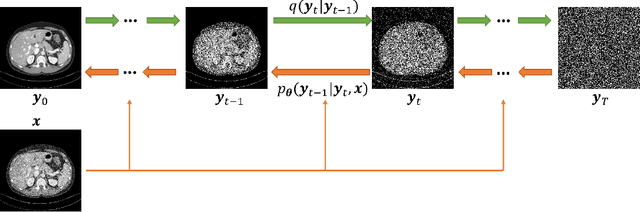
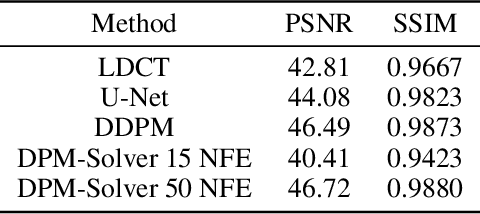
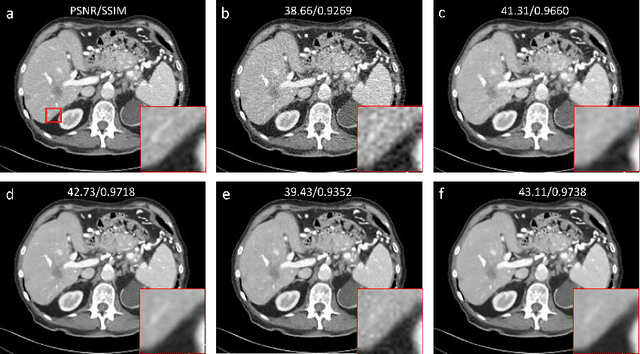

Low-dose computed tomography (LDCT) is an important topic in the field of radiology over the past decades. LDCT reduces ionizing radiation-induced patient health risks but it also results in a low signal-to-noise ratio (SNR) and a potential compromise in the diagnostic performance. In this paper, to improve the LDCT denoising performance, we introduce the conditional denoising diffusion probabilistic model (DDPM) and show encouraging results with a high computational efficiency. Specifically, given the high sampling cost of the original DDPM model, we adapt the fast ordinary differential equation (ODE) solver for a much-improved sampling efficiency. The experiments show that the accelerated DDPM can achieve 20x speedup without compromising image quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge