Low-dimensional Data Embedding via Robust Ranking
Paper and Code
May 16, 2017
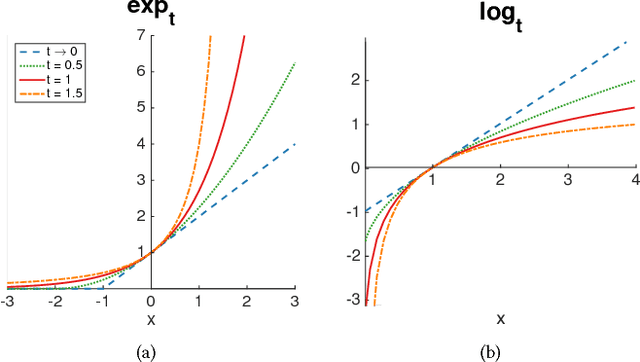
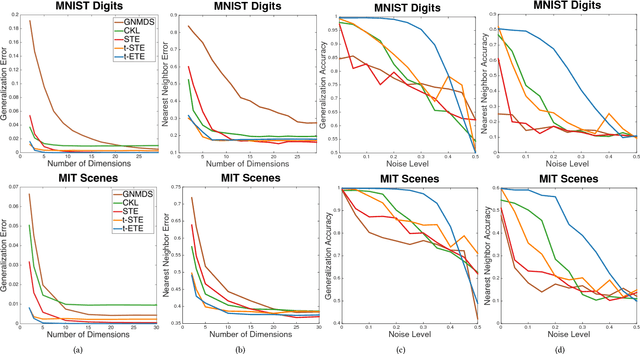
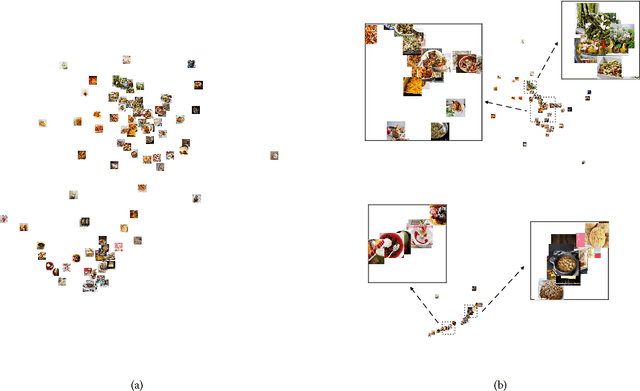
We describe a new method called t-ETE for finding a low-dimensional embedding of a set of objects in Euclidean space. We formulate the embedding problem as a joint ranking problem over a set of triplets, where each triplet captures the relative similarities between three objects in the set. By exploiting recent advances in robust ranking, t-ETE produces high-quality embeddings even in the presence of a significant amount of noise and better preserves local scale than known methods, such as t-STE and t-SNE. In particular, our method produces significantly better results than t-SNE on signature datasets while also being faster to compute.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge