Loss-Optimal Classification Trees: A Generalized Framework and the Logistic Case
Paper and Code
Jun 01, 2023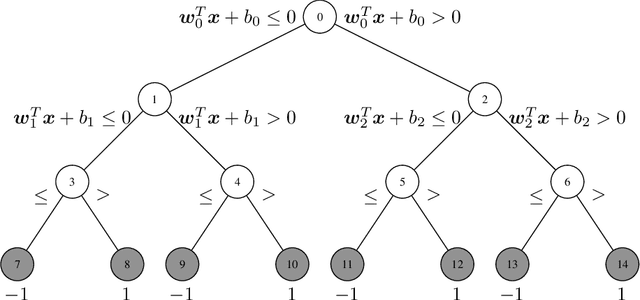

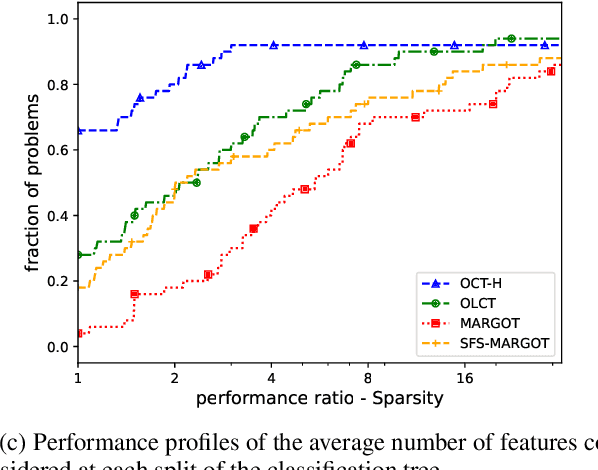
The Classification Tree (CT) is one of the most common models in interpretable machine learning. Although such models are usually built with greedy strategies, in recent years, thanks to remarkable advances in Mixer-Integer Programming (MIP) solvers, several exact formulations of the learning problem have been developed. In this paper, we argue that some of the most relevant ones among these training models can be encapsulated within a general framework, whose instances are shaped by the specification of loss functions and regularizers. Next, we introduce a novel realization of this framework: specifically, we consider the logistic loss, handled in the MIP setting by a linear piece-wise approximation, and couple it with $\ell_1$-regularization terms. The resulting Optimal Logistic Tree model numerically proves to be able to induce trees with enhanced interpretability features and competitive generalization capabilities, compared to the state-of-the-art MIP-based approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge