LoRA-Pro: Are Low-Rank Adapters Properly Optimized?
Paper and Code
Jul 25, 2024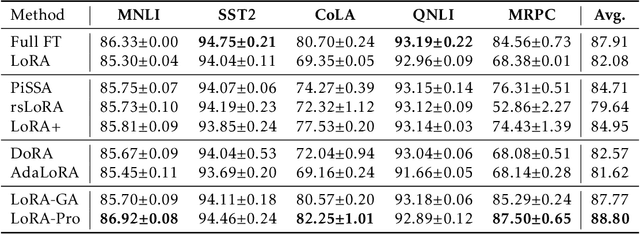
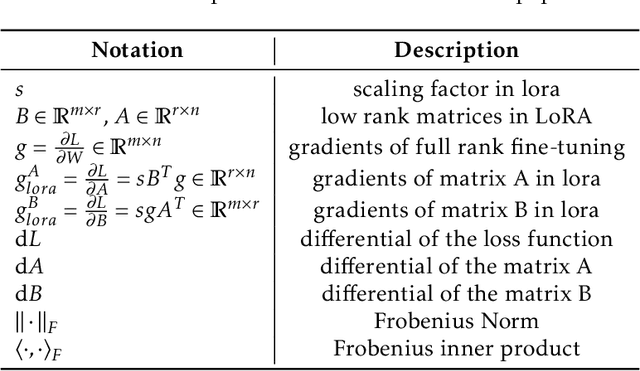
Low-Rank Adaptation, also known as LoRA, has emerged as a prominent method for parameter-efficient fine-tuning foundation models by re-parameterizing the original matrix into the product of two low-rank matrices. Despite its efficiency, LoRA often yields inferior performance compared to full fine-tuning. In this paper, we propose LoRA-Pro to bridge this performance gap. Firstly, we delve into the optimization processes in LoRA and full fine-tuning. We reveal that while LoRA employs low-rank approximation, it neglects to approximate the optimization process of full fine-tuning. To address this, we introduce a novel concept called the "equivalent gradient." This virtual gradient makes the optimization process on the re-parameterized matrix equivalent to LoRA, which can be used to quantify the differences between LoRA and full fine-tuning. The equivalent gradient is derived from the gradients of matrices $A$ and $B$. To narrow the performance gap, our approach minimizes the differences between the equivalent gradient and the gradient obtained from full fine-tuning during the optimization process. By solving this objective, we derive optimal closed-form solutions for updating matrices $A$ and $B$. Our method constrains the optimization process, shrinking the performance gap between LoRA and full fine-tuning. Extensive experiments on natural language processing tasks validate the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge